Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

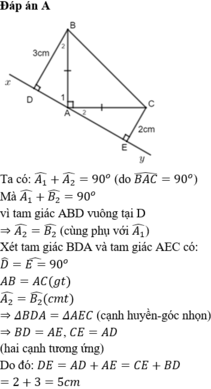
Xét \(\Delta BAD\)và \(\Delta AEC\) có :
\(\widehat{BDA}=\widehat{AEC}\left(=90^o\right)\)
AB = AC ( gt)
\(\widehat{BAD}=\widehat{AEC}\)( cùng phụ với góc EAC)
suy ra \(\Delta ABD=\Delta AEC\)( cạnh huyền góc nhọN)

a) Xét ∆BAD và ∆ACE có:
^BDA=^AEC (cùng bằng 90 độ)
AB=AC (gt)
^BAD=^ACE (cùng phụ với ^EAC)
suy ra ∆BAD=∆ACE (cạnh huyền-góc nhọn)
b) Do ∆BAD=∆ACE nên AD=CE và AE=BD
mà DE=DA+AE
suy ra DE = CE+BD (đpcm)
b) Có: BAP + PAC = 90o
t/g BPA vuông tại P có: ABP + BAP = 90o
Suy ra PAC = ABP
Xét t/g BPA vuông tại P và t/g AQC vuông tại Q có:
AB = AC (gt)
ABP = CAQ (cmt)
Do đó, t/g BPA = t/g AQC ( cạnh huyền - góc nhọn)
=> AP = QC (2 cạnh tương ứng)
và BP = AQ (2 cạnh tương ứng)
= AP + PQ = QC + PQ
=> PQ = BP - QC (đpcm)

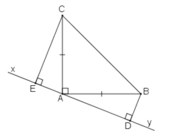
Ta có: ΔAEC= ΔBDA
⇒AE = BD và EC = DA
Mà DE = DA + AE
Vậy: DE = CE + BD