Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Dựng ΔADE 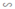 ΔABC theo tỉ số 2/3
ΔABC theo tỉ số 2/3
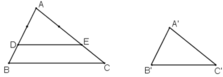
Trên AB lấy D, trên AC lấy E sao cho 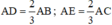
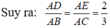
Khi đó theo định lý Ta-let đảo ta suy ra DE // BC
⇒ ΔADE 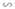 ΔABC theo tỉ số 2/3.
ΔABC theo tỉ số 2/3.
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc 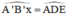
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
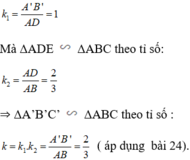

Giải:
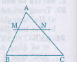
Trên cạnh AB lấy điểm M sao cho AM= 2323AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=2323
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)

a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).

Sửa đề: ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
Vì ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
mà ΔA'B'C' \(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_2=\dfrac{3}{4}\)
nên ΔABC\(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_1\cdot k_2=\dfrac{2}{3}\cdot\dfrac{3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
hay ΔA"B"C"\(\sim\)ΔABC theo tỉ số đồng dạng k=2

b: Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(đồng vị, MN//BC)
góc A chung
Do đó: ΔAMN\(\sim\)ΔABC

Bài 2 :
vì BE vuông góc BD nên BE là đường phân giác ngoài của tam giác ABC.
theo tính chất đường phân giác (ngoài) ta có :
AEEB=ECBCAEEB=ECBC
⇒⇒ CE=AB.BCABCE=AB.BCAB
⇒⇒ CE=AE.23CE=AE.23
⇒⇒ 3CE=(CE+AC).23CE=(CE+AC).2
⇒⇒ 3CE=2CE+2AC3CE=2CE+2AC
⇒⇒ CE=2AC=6(cm)
Bài 1: Giải
Nếu cạnh lớn nhất của tam giác đã cho là cạnh bé nhất của tam giác đồng dạng với nó thì ta có tỉ số đồng dạng đã cho là: (Gọi tạm tam giác có cạnh 12,16,18 m là tgiac 1, tgiac mới là tgiac 2)
k=Δ1Δ2=1218=23k=Δ1Δ2=1218=23
Chu vi của tam giác 1 là:
12+16+18=46(m)12+16+18=46(m)
⇒⇒ Chu vi của tam giác 2 là: 46:23=69(m)46:23=69(m)
Cạnh thứ hai của tam giác đồng dạng (2) là:
16:23=24(m)16:23=24(m)
Cạnh lớn nhất của tam giác đồng dạng (2) đó là:
69−24−18=27(m
Bài 3 tớ k bt lm
Tam giác A'B'C' có AB/A'B'=1/3, BC/B'C'=1/3, AC/A'C'=1/3.