Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: ˆBAH=ˆBAC+ˆCAH=ˆBAC+900
ˆEAC=ˆBAC+ˆBAE=ˆBAC+900
Suy ra: ˆBAH=ˆEAC
– Xét ∆ BAH và ∆ EAC:
BA = EA (vì ABDE là hình vuông)
ˆBAH=ˆEAC (chứng minh trên)
AH = AC (vì ACFH là hình vuông)
Do đó: ∆ BAH = ∆ EAC (c.g.c)
⇒ BH = EC
Gọi giao điểm của EC với AB và BH lần lượt là K và O.
ˆAEC=ˆABH (vì ∆ BAH = ∆ EAC) (1)
hay ˆAEK=ˆOBK
– Trong ∆ AEK ta có: ˆEAK=900
⇒ˆAEK+ˆAKE=900

* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.

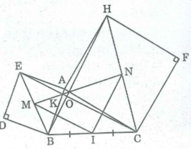
Hình đa giác TenDaGiac1: DaGiac[B, A, 4] Hình đa giác TenDaGiac2: DaGiac[A, C, 4] Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng i: Đoạn thẳng [B, A] của Hình đa giác TenDaGiac1 Đoạn thẳng j: Đoạn thẳng [A, E] của Hình đa giác TenDaGiac1 Đoạn thẳng k: Đoạn thẳng [E, D] của Hình đa giác TenDaGiac1 Đoạn thẳng l: Đoạn thẳng [D, B] của Hình đa giác TenDaGiac1 Đoạn thẳng m: Đoạn thẳng [A, C] của Hình đa giác TenDaGiac2 Đoạn thẳng n: Đoạn thẳng [C, F] của Hình đa giác TenDaGiac2 Đoạn thẳng p: Đoạn thẳng [F, H] của Hình đa giác TenDaGiac2 Đoạn thẳng q: Đoạn thẳng [H, A] của Hình đa giác TenDaGiac2 Đoạn thẳng r: Đoạn thẳng [E, C] Đoạn thẳng s: Đoạn thẳng [B, H] Đoạn thẳng d: Đoạn thẳng [O1, O2] Đoạn thẳng e: Đoạn thẳng [O2, I] Đoạn thẳng f_1: Đoạn thẳng [O1, I] A = (-0.2, 4.86) A = (-0.2, 4.86) A = (-0.2, 4.86) B = (-1, 1.46) B = (-1, 1.46) B = (-1, 1.46) C = (4.56, 0.9) C = (4.56, 0.9) C = (4.56, 0.9) Điểm E: DaGiac[B, A, 4] Điểm E: DaGiac[B, A, 4] Điểm E: DaGiac[B, A, 4] Điểm D: DaGiac[B, A, 4] Điểm D: DaGiac[B, A, 4] Điểm D: DaGiac[B, A, 4] Điểm F: DaGiac[A, C, 4] Điểm F: DaGiac[A, C, 4] Điểm F: DaGiac[A, C, 4] Điểm H: DaGiac[A, C, 4] Điểm H: DaGiac[A, C, 4] Điểm H: DaGiac[A, C, 4] Điểm O2: Giao điểm của b, c Điểm O2: Giao điểm của b, c Điểm O2: Giao điểm của b, c Điểm O1: Giao điểm của t, a Điểm O1: Giao điểm của t, a Điểm O1: Giao điểm của t, a Điểm I: Trung điểm của g Điểm I: Trung điểm của g Điểm I: Trung điểm của g
a. Ta thấy \(\widehat{EAC}=\widehat{BAH}\left(=\widehat{BAC}+90^o\right)\)
Vậy nên \(\Delta EAC=\Delta BAH\left(c-g-c\right)\)
Từ đó suy ra \(\widehat{ACE}=\widehat{AHB}\)
Vì \(\widehat{AHB}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{ACE}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{HJC}=90^o\)
Vậy \(EC\perp BH.\)
b. Ta thấy \(O_1\) là trung điểm EB. Vậy thì O1I là đường trung bình của tam giác BEC hay O1I // EC. Tương tự O2I // BH.
Lại có \(EC\perp BH\) nên \(O_1I\perp O_2I.\)
Vậy tam giác O1O2I là tam giác vuông tại I.
