Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu tam giác là t/g nhé
a) Có: BE _|_ Ax (gt)
CF _|_ Ax (gt)
Suy ra BE // CF (1)
Xét t/g EMB vuông tại E và t/g FMC vuông tại F có:
BM = CM (gt)
EMB = FMC ( đối đỉnh)
Do đó, t/g EMB = t/g FMC ( cạnh huyền và góc nhọn kề)
=> BE = CF (2 cạnh tương ứng) (2)
ME = MF (2 cạnh tương ứng) (3)
(1); (2) và (3) là đpcm
b) Xét t/g EMC và t/g FMB có:
EM = MF (câu a)
EMC = FMB ( đối đỉnh)
CM = BM (gt)
Do đó, t/g EMC = t/g FMB (c.g.c)
=> CE = BF (2 cạnh tương ứng) (4)
ECM = FBM (2 góc tương ứng)
Mà ECM và FBM là 2 góc so le trong
Nên EC // BF (5)
(4) và (5) là đpcm

a: Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF

câu sai nha bạn người ta bảo điều kiện của tam giác abc chứ ko phải thay canh BE với CE nha

a, Ta có: BE vuông Ax(1)
CF vuông Ax(2)
Từ (1) và (2) => BE//CF
b,Tam giác BEM = Tam giác CFM(g.c.g)
=>BE=CF(các cạnh tương ứng)
Chứng minh tương tự ta đươc: Tam giác CME = Tam giác BMF (c.g.c)
=> CE=BF(các cạnh tương ứng)
c,Nếu BE=CE
thì tam giác BEC cân tại E
mà E thuộc AM
AM là đg trug tuyến
thì khi cân cũng sẽ là đg cao
nên khi tam giác ABC cân tại A THÌ BE=CE

Chẳng hiểu gì.Hỏi cô Thủy hoặc thầy Phong hoặc thầy Huy.Không thì vào goodgle.

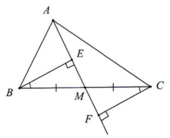
Giải thích các bước giải:
BE ⊥ AM, CF⊥AM
=> BE // CF
a) Xét Δ vuông BME và Δ vuông CMF có:
BM = MC ( M là tđ BC )
B1 = C1 ( so le trong )
=> Δ ... = Δ ... ( ch - gn)
b) ME = MF ( cạnh tương ứng )
c) Xét Δ MEC và Δ MFB có:
M1 = M2 (đối đỉnh)
ME = MF (cmt)
BM = CM (cmt)
=> Δ ... = Δ ... ( cgc )
=> CE = BF
d)
Ta có: C2 = B2 (Δ MEC = Δ MFB)
Mà 2 góc này ở vị trí so le trong
=> CE // BF