Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABM và ΔDEN có
AB=DE
\(\widehat{B}=\widehat{E}\)
BM=EN
Do đó: ΔABM=ΔDEN
Suy ra: AM=DN
Ta có:
ΔABC=ΔDEF(gt)ΔABC=ΔDEF(gt)
⇒⎧⎪⎨⎪⎩AB=DEˆABC=ˆABM=ˆDEF=ˆDENBC=EF⇒{AB=DEABC^=ABM^=DEF^=DEN^BC=EF
Ta lại có:
⎧⎪ ⎪⎨⎪ ⎪⎩BM=MC=12BC(gt)EN=NF=12EF(gt){BM=MC=12BC(gt)EN=NF=12EF(gt)
⇒BM=MC=EN=NF⇒BM=MC=EN=NF
Xét ΔABMΔABM và ΔDENΔDEN có:
AB=DE(ΔABC=ΔDEF)AB=DE(ΔABC=ΔDEF)
ˆABM=ˆDEN(cmt)ABM^=DEN^(cmt)
BM=EN(cmt)BM=EN(cmt)
Do đó ΔABM=ΔDEN(c.g.c)ΔABM=ΔDEN(c.g.c)
⇒AM=DN (Hai cạnh tương ứng)
sr bạn mình ko bk vẽ hình trên đây

Giải
a) vì m la trung diểm của BC => BM=MC
Xét tam giac BAM va tam giac MAC có:
AB=AC(dề bài cho)
BM=MC(Chung minh tren)
AM la cạnh chung(de bai cho)
=>Tam giác BAM=tam giac MAC(c.c.c)
b)từ trên
=>góc BAM=góc MAC(hai goc tuong ung)
Tia AM nam giua goc BAC (1)
goc BAM=goc MAC(2)
từ (1) va (2)
=>AM la tia phan giac cua goc BAC
c)Còn nữa ......-->

A B C D E M N
( GT, KL bạn tự viết nha )

Ý C là ghi sai đề bài rồi nhé
Còn ý d khó nhất thì giải như sau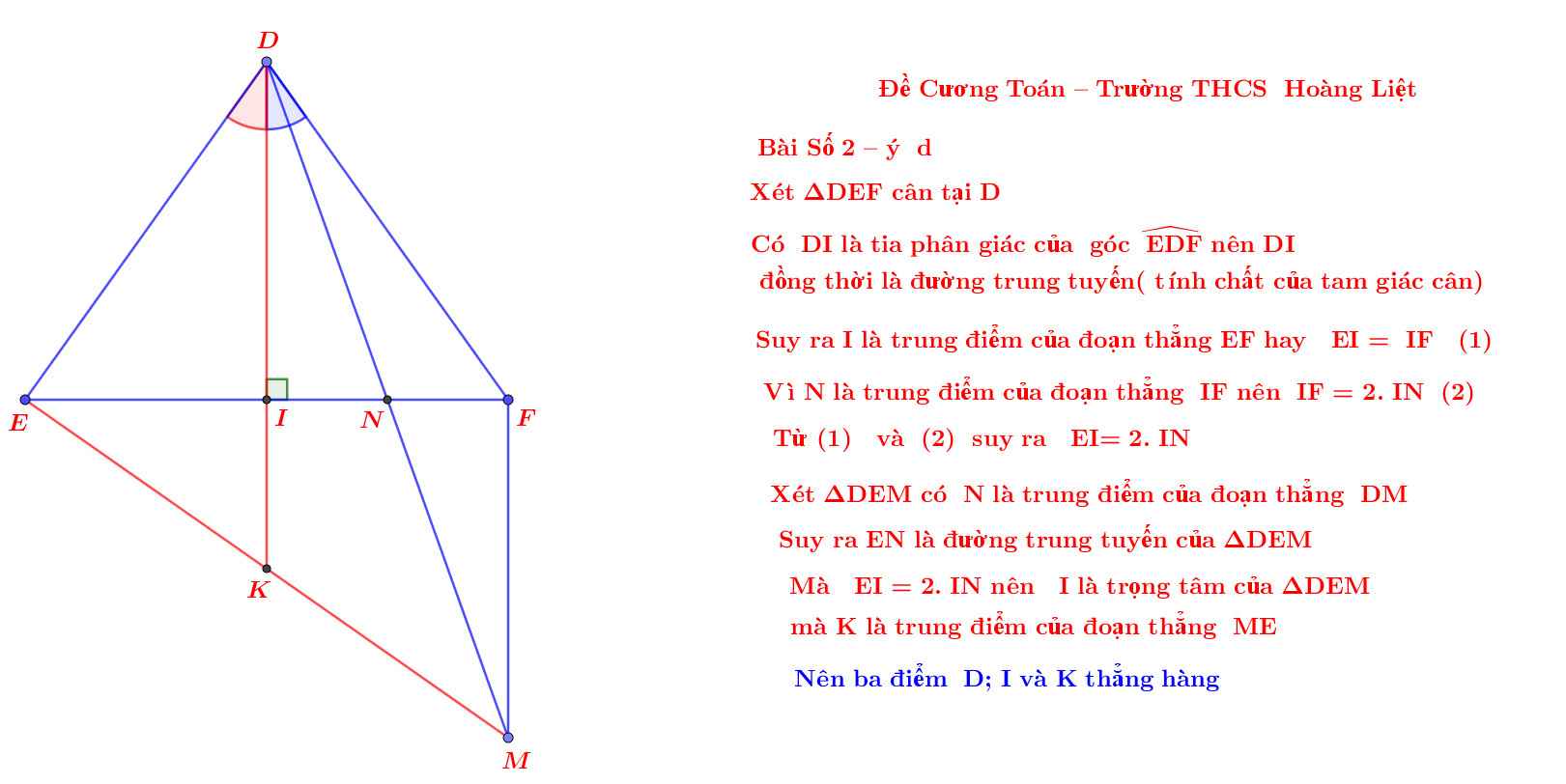

Trên tia đối tia AM lấy điểm C sao cho AM=MD
Xét tam giác ABM=tam giác DCM (c-g-c)
\(\Rightarrow\)AB=CD (2 cạnh tương ứng)
\(\Rightarrow\)\(\widehat{ABM}=\widehat{MDC}\)(2 góc tương ứng)
Ta có AB<AC (gt) mà AB=CD (cmt) suyra CD<AC
\(\Rightarrow\)\(\widehat{MDC}>\widehat{MAC}\)mà \(\widehat{BAM}=\widehat{MDC}\)
\(\Rightarrow\)\(\widehat{BAM}>\widehat{MAC}\)(ĐPCM)
a)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các cặp cạnh tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) BC = EF
\(\Rightarrow\) BM = EN (vì BM = BC/2, EN = EF/2 (1)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các góc tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) Góc ABC = EFBC = góc DEF (2)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các cặp cạnh tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) AB = DE
+ Xét hai tam giác BAM và tam giác DEN, ta có:
\(\left\{{}\begin{matrix}BM=EM\\\widehat{ABC}=\widehat{DEF}\\AB=DE\end{matrix}\right.\)
nên hai tam giác BAM và tam giác DEN bằng nhau theo trường hợp cạnh - góc - cạnh.
b)
+ Có \(\left\{{}\begin{matrix}\Delta ABC=\Delta DEF\\\Delta ABM=\Delta DEN\end{matrix}\right.\)
nên \(\Delta ABC-\Delta ABM=\Delta DEF-\Delta DEN\)
\(\Rightarrow\) Hai tam giác AMC và tam giác DNF bằng nhau.
\(\Rightarrow\) Hai góc MAC và góc NDF tương ứng bằng nhau.
Mong cái này giúp được bạn nhé. ☺