Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

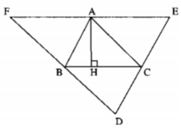
F A E B C D
(thông cảm chút vì hình xấu :< )
Xét ΔABC và ΔACE, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔACE (g.c.g)
⇒ AE = BC (1)
Xét ΔABC và ΔABF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.
b. Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.

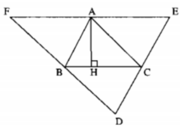
Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.

Xét ΔABC và ΔCEA, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔCEA (g.c.g)
⇒ BC = AE (1)
Xét ΔABC và ΔBAF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.

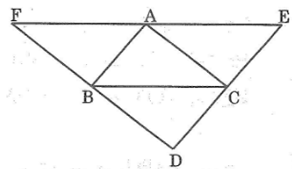
A B C D E F H I K
DE//BC, AH vuông góc BC => AH vuông góc DE (Qhệ //, vuông góc) (1)
BC//AD, AC//BD => BC=AD, AC=BD (T/c đoạn chắn), tương tự BC=AE => BC=AD=AE (2)
Từ (1) và (2) => AH là trung trực của DE.
Tương tự với các cạnh của tam giác DEF và đường cao của tam giác ABC, ta có:
BI vuông góc DF, AC=BD=BF => BI là trung trực của DF
CK vuông góc EF, AB=CE=CF => CK là trung trực của EF.
Kết luận:...


a,
Theo bài ra ta có:
+)FE//BC
+)EC//BA hay ED//BA
+)AC//FB hay AC//FD
Khi đó:
+)\(\widehat{FBA}=\widehat{BAC}\)
+)\(\widehat{B\text{AF}}=\widehat{ABC}\)
Vì BF//AC
Xét \(\Delta FBA\) và \(\Delta CAB\) có:
\(\left\{{}\begin{matrix}\widehat{B\text{AF}}=\widehat{ABC}\\BAchung\\\widehat{FBA}=\widehat{BAC}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA\) = \(\Delta CAB\) (g.c.g)
=> FB=AC ( hai cạnh tương ứng )
Ta lại có:
+) \(\widehat{FAB}=\widehat{CEA}\)
+) \(\widehat{BFA}=\widehat{CAE}\)
( vì BF//CA và BA//CE )
=> \(\widehat{FBA}=\widehat{ACE}\)
Xét \(\Delta FBA\) và \(\Delta ACE\) có:
\(\left\{{}\begin{matrix}\widehat{BFA}=\widehat{CAE}\\FB=AC\\\widehat{FBA}=\widehat{ACE}\end{matrix}\right.\) (cmt)
=> \(\Delta FBA=\Delta ACE\left(g.c.g\right)\)
=> FA=EA ( hai cạnh tương ứng )
Mà F;A;E thẳng hàng
=> A là trung điểm của EF
(đ.p.c.m)
b,
Các đường cao của tam giác ABC là các đường trung trực của tam giác DFE
Xét ΔABC và ΔACE, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔACE (g.c.g)
⇒ AE = BC (1)
Xét ΔABC và ΔABF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.
b. Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.