Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em kham khảo link này nhé.
Câu hỏi của Trần Đức Thắng - Toán lớp 9 - Học toán với OnlineMath

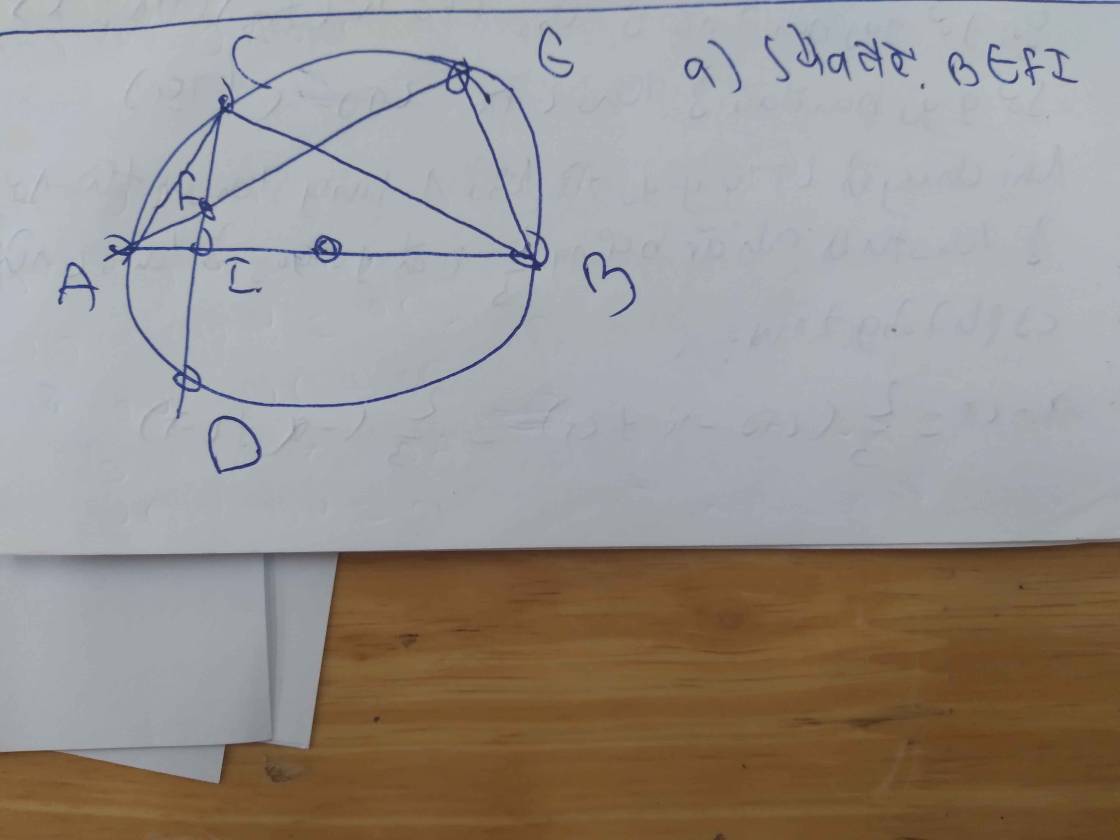
a)
AC=AB=> A thuộc tt BC (1)
BD=CD=>D thuộc tt BC (2)
Từ (1);(2) ta suy ra: AD là tt BC
=> AD vuông góc BC mà H là giao BC
=> AH vuông góc BC
Tg ABH là nửa tg đều nên AH= (căn 3.a)/2= (căn 3.căn 3.4)/2=6 cm
Tg ACD nội tiếp (O) đg kính AD=> Tg ACD vuông tại C
CH^2=AH.HD=>HD= 12/6=2
=> AD=6+2=8
Vì AD=2R=>R=4
Hok tốt !
mk gợi ý phần b nhé,
dẽ dàng nói đc tam giác AOC cân tại O =) góc AOE=góc COE =) có thể chứng minh đc tam giác AOE = tam giác COE(c-g-c)
=) EC vuông góc với OC =) đpcm
tiếp tục gọi giao điểm của AC với BE là M =) cm đc tam giác AME = tam giác CMB ( dựa vào AE//BC) =) AE = BC =) tứ giác AECB là hình bình hành
mà AB=BC =) tứ giác AECB là hình thoi


bài này dễ mà mai mik làm cho nha
Câu a) tự làm nhé ==* chưa làm được
A E B F C D c a b
Gọi F là tiếp điểm của đường tròn (I) với BC.
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
AE = AD
BE = BF
CD = CF
Mà: AE = AB – BE
AD = AC – CD
Nên: AE + AD = ( AB – BE ) + ( AC – CD ) = AB + AC – ( BE + CD )
= AB + AC – (BF + CF) = AB + AC – BC
Suy ra: AE + AD = c + b – a
Hay: AE = AD = \(\frac{\left(c+b-a\right)}{2}\)