Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE

a: Ta có: ΔBKC vuông tại K
mà KM là đường trung tuyến
nên KM=BC/2(1)
Ta có: ΔBHC vuông tại H
mà HM là đường trung tuyến
nên HM=BC/2(2)
Từ (1)và (2) suy ra MH=MK
hay ΔMHK cân tại M
b: Kẻ MN vuông góc với HK
=>N là trung điểm của HK
Xét hình thang CBDE có
M là trung điểm của BC
MN//DB//EC
DO đó: N là trung điểm của DE
=>DK=HE

a) Xét ΔBCK vuông tại K có KM là trung tuyến ⟹KM=1/2BC
Xét ΔBCH vuông tại K có HM là trung tuyến ⟹HM=1/2BC
⟹KM=HM⟹ΔHKM cân tại M
b) Kẻ MN⊥DE(N∈DE)
Ta có: BD⊥DE;CE⊥DE⟹BD//CE
⟹BDEC là hình thang
Xét hình thang BDEC có: MN⊥DE⟹MN//CE;BM=CM(gt)⟹DN=EN=EN
Mặt khác, ΔKHMΔKHM là tam giác cân có MN⊥DE⟹MN
Trừ theo vế (1) và (2) ta có: DN−KN=EN−HN⟹DK=HE

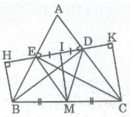
* Ta có: BH ⊥ DE (gt)
CK ⊥ DE (gt)
⇒ BH // CK hay tứ giác BHKC là hình thang
Gọi M là trung điểm của BC, I là trung điểm của DE
* Trong tam giác BDC vuông tại D có DM là trung tuyến ứng với cạnh huyền BC.
⇒ DM = 1/2 BC (tính chất tam giác vuông)
* Trong tam giác BEC vuông tại E có EM là đường trung tuyến ứng với cạnh huyền BC.
⇒ EM = 1/2 BC (tính chất tam giác vuông)
Suy ra: DM = EM nên ΔMDE cân tại M
MI là đường trung tuyến nên MI là đường cao ⇒ MI ⊥ DE
Suy ra: MI // BH // CK
BM = MC
Suy ra: HI = IK (tính chất đường trung bình hình thang)
⇒ HE + EI = ID + DK
Mà EI = ID nên EH = DK