Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

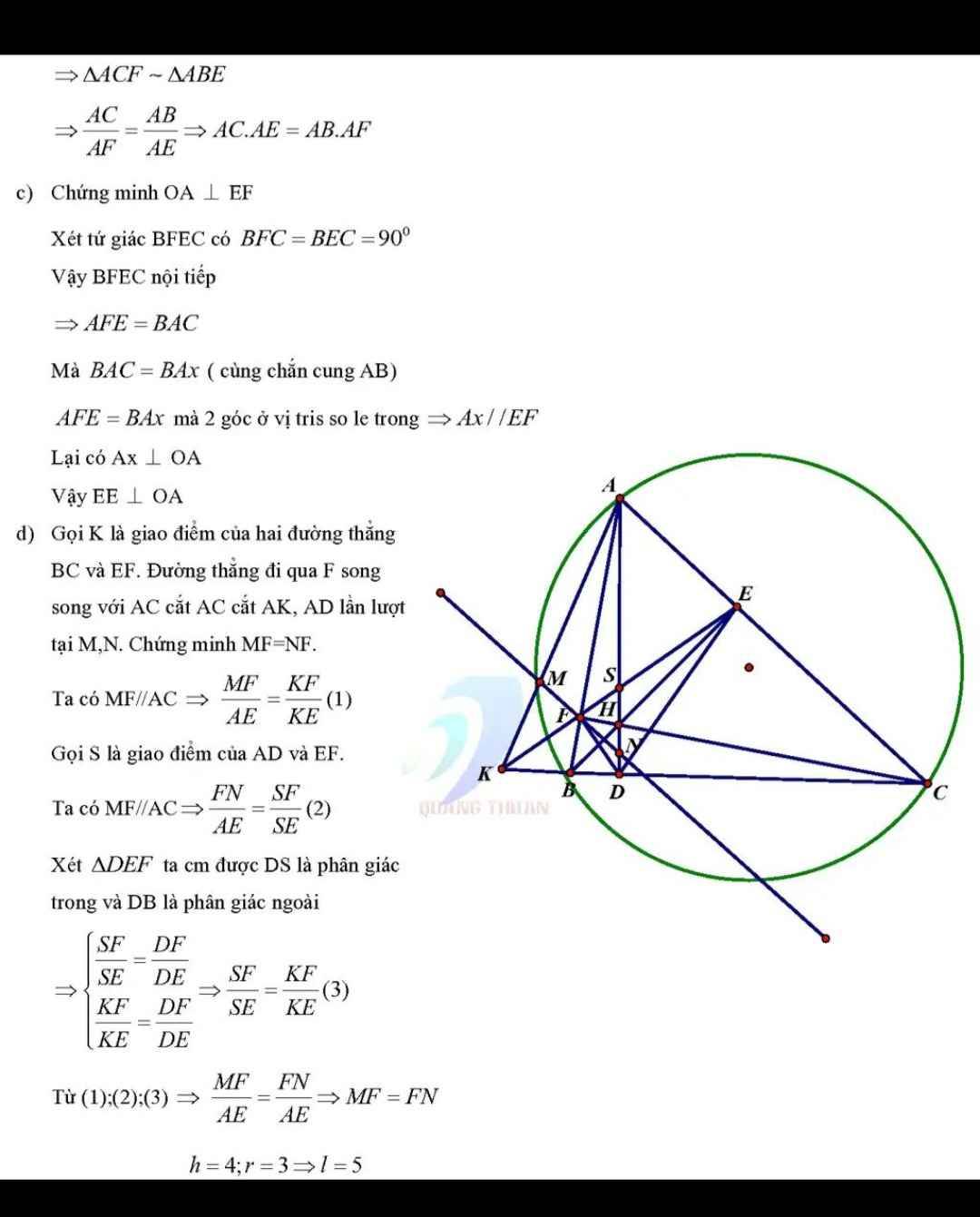
A B C G F E D Q P
a) Ta dễ thấy ^ABF = ^BAF = ^BAD = ^CAD = ^ACE = ^CAE. Suy ra \(\Delta\)ABF ~ \(\Delta\)ACE (g.g) (đpcm).
b) Gọi BE cắt CF tại G. Áp dụng hệ quả ĐL Thales, kết hợp với \(\Delta\)ABF ~ \(\Delta\)ACE ta có:
\(\frac{GC}{GF}=\frac{CE}{FB}=\frac{AC}{AB}\). Mà \(\frac{AC}{AB}=\frac{DC}{DB}\)(ĐL đường phân giác trong tam giác) nên \(\frac{GC}{GF}=\frac{DC}{DB}\)
Do đó GD // BF // CE (ĐL Thales đảo). Lại có AD // BF // CE nên A,G,D thẳng hàng
Vậy thì AD,BE,CF cắt nhau tại G (đpcm).
c) Chú ý GQ // AE suy ra ^AGQ = ^GAE = ^GAF, đồng thời có AG // QF. Suy ra AFQG là hình thang cân (1)
Mặt khác BF // CE dẫn đến ^GFQ = ^GCE = ^GPQ. Từ đây bốn điểm P,Q,F,G cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra các điểm A,P,G,Q,F cùng thuộc một đường tròn (đpcm).


a) Chứng minh ΔABF ~ ΔACE
\(\odot\) Ta có: FA = FB (F ∈ đường trung trực của AB)
⇒ ΔFAB cân tại F
Tương tự, ta cũng có ΔEAC cân tại E
\(\odot\) Mặt khác:
\(\widehat{FBA}=\widehat{BAD}\) (AD // BF, 2 góc so le trong)
\(\widehat{BAD}=\widehat{CAD}\) (AD là tia phân giác của \(\widehat{BAC}\))
\(\widehat{CAD}=\widehat{ECA}\) (AD // CE, 2 góc so le trong)
\(\Rightarrow\widehat{FBA}=\widehat{ECA}\)
\(\odot\) Suy ra ΔFAB cân tại F và ΔEAC cân tại E có \(\widehat{FBA}=\widehat{ECA}\)
⇒ ΔFAB ~ ΔEAC
b) Chứng minh AD, BE, CF đồng quy
\(\odot\) Gọi G là giao điểm của BE và CF. Ta sẽ chứng minh A, G, D thẳng hàng.
\(\odot\) Theo định lí Thales: BF // EC (do cùng song song với AD)
\(\Rightarrow\dfrac{FG}{GC}=\dfrac{BF}{CE}\)
\(\odot\) Mà:
\(\dfrac{BF}{CE}=\dfrac{AB}{AC}\) (ΔFAB ~ ΔEAC)
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (AD là đường phân giác của ΔABC)
\(\odot\) Suy ra \(\dfrac{FG}{GC}=\dfrac{BD}{CD}\)
Theo định lí Thales đảo ⇒ GD // BF
mà AD // BF (gt) nên \(AD\equiv GD\)
⇒ A, G, D thẳng hàng
⇒ đpcm
c) Chứng minh A, P, G, Q, F đồng viên
\(\odot\) Ta có: \(\widehat{FAG}=\widehat{EAG}\)
mà \(\widehat{EAG}=\widehat{QGA}\) (2 góc so le trong, QG // AE)
\(\Rightarrow\widehat{FAG}=\widehat{QGA}\)
mà FAGQ là hình thang
⇒ FAGQ là hình thang cân
⇒ FAGQ nội tiếp (1)
\(\odot\) Mặt khác: ECGP nội tiếp
\(\Rightarrow\widehat{CEP}=\widehat{PGF}\) (cùng bù \(\widehat{PGC}\))
mà \(\widehat{CEP}=\widehat{FQP}\) (2 góc so le trong, BF // CE)
\(\Rightarrow\widehat{PGF}=\widehat{FQP}\)
⇒ FQGP nội tiếp (2)
\(\odot\) Từ (1) và (2) ⇒ Ngũ giác AFQGP nội tiếp
⇒ đpcm

Gọi G là giao điểm của FC và AK.
Áp dụng định lý Menelaus cho tam giác FBC với cát tuyến A, G, K ta có:
\(\dfrac{AF}{AB}.\dfrac{KB}{KC}.\dfrac{GC}{GF}=1\Rightarrow\dfrac{GC}{GF}=\dfrac{KC}{KB}.\dfrac{AB}{AF}\). (1)
Áp dụng định lý Menelaus cho tam giác ACB với cát tuyến K, E, F ta có:
\(\dfrac{EA}{EC}.\dfrac{KC}{KB}.\dfrac{FB}{FA}=1\Rightarrow\dfrac{KC}{KB}=\dfrac{FA}{FB}.\dfrac{EC}{EA}\). (2)
Từ (1), (2) có \(\dfrac{GC}{GF}=\dfrac{EC}{EA}.\dfrac{AB}{FB}\). (*)
Mặt khác áp dụng định lý Menelaus cho tam giác AFC với cát tuyến B, H, E ta có:
\(\dfrac{HC}{HF}.\dfrac{BF}{BA}.\dfrac{EA}{EC}=1\Rightarrow\dfrac{HC}{HF}=\dfrac{AB}{FB}.\dfrac{EC}{EA}\). (**)
Từ (*), (**) ta có \(\dfrac{GC}{GF}=\dfrac{HC}{HF}\Rightarrow\dfrac{AC}{MF}=\dfrac{AC}{NF}\Rightarrow FM=FN\).

\({}\)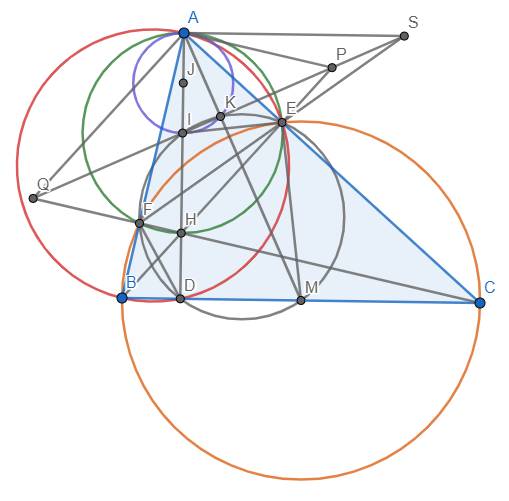
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)

A B C D I R H K J M N O
Gọi M, N lần lượt là chân đường cao hạ từ B,C xuống AC,AB
Ta có \(DH.DA=DB.DC\)(1)
Để chứng minh K là trực tâm tam giác IBC ta chứng minh \(DK.DJ=DB.DC\)hay \(DK.DJ=DH.DA\)
Ta có NC,NA lần lượt là phân giác trong và phân giác ngoài của \(\widehat{MND}\)nên
\(\frac{HK}{HD}=\frac{NK}{ND}=\frac{AK}{AH}\)
\(\Rightarrow AK.HD=AD.HK\)
\(\Leftrightarrow HD\left(AD-DK\right)=AD\left(DK-DH\right)\)
\(\Leftrightarrow2.AD.DH=DK\left(DA+DH\right)\)
\(\Leftrightarrow2.AD.DH=2.DK.DJ\)
\(\Rightarrow AD.DH=DK.DJ\left(2\right)\)
Từ (1) và (2) ta có\(DK.DJ=DH.DA\)
=> K là trực tâm của tam giác IBC