Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi D là giao của AC và HH'
=>HD=H'D
=>ΔAHH' cân tại A
=>góc AHH'=góc AHD=góc ACB
=>AH'CB là tứ giác nội tiếp

bạn tự vẽ hình nhé !
Giải
a,Ta có :\(\widehat{BAB'}=\widehat{AB'A'}=\widehat{B'A'B}=1v\)( nội tiếp nửa đường tròn )
\(\Rightarrow ABA'B'\)là hình chữ nhật
b, Ta có : BH // CA' (cùng vuông góc với AC )
BA' // CH ( cùng vuông góc với AB )
\(\Rightarrow BHCA'\)là hình bình hành nên BH = CA'
c, \(\Delta BHC=\Delta BA'C\)nên đường tròn ngoại tiếp tam giác BHC bằng đường tròn ngoại tiếp tam giác BA'C
Mà đường tròn ngoại tiếp tam giác BA'C chính là đường tròn (O)
Vậy bán kính đường tròn ngoại tiếp tam giác BHC bằng R
a) tứ giác ABA'B' có AA', BB' là hai đương chéo bằng nhau ( = 2R)
=> ABA'B' là hình chữ nhật.
b) ta có :
CH _I_ AB ( H là trực tâm của tam giác ABC )
A'B _I_ AB ( ABA' chắn nửa đường tròn )
=> CH // A'B (1)
Lại có :
BH _I_ AC ( H là trực tâm của tam giác ABC )
A'C _I_ AC ( ACA' chắn nửa đường tròn )
=> A'C // BH (2)
(1),(2) => BHCA' là hình bình hành
=> BH=CA'
c) kéo dài AH cắt đường tròn ngoại tiếp ABC tại D. Dễ dàng nhận thấy D và H đối xứng nhau qua BC ---> tam giác BCD = tam giác BCH --> đường tròn ngoại tiếp BCH = đường tròn ngoại tiếp BCD (đồng thời ngoại tiếp ABC) --> bán kính đường tròn ngoại tiếp BHC = R

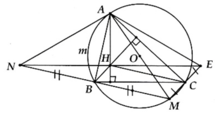
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
A E F H O D B H' A' C
a . Gọi AH ∩ BC=D,BH ∩ AC=E,CH ∩ AB=F
\(\Rightarrow AD\perp BC,BE\perp AC,CF\perp AB\)
\(\Rightarrow\widehat{ADC}=\widehat{AFC}=90^0\) => ◊AFDC nội tiếp
\(\Rightarrow\widehat{DCF}=\widehat{DAF}\)
VÌ H đối xứng H' qua BC
\(\Rightarrow HH'\perp BC\Rightarrow A,H,,D,H'\)thẳng hàng
\(\Rightarrow\widehat{BAH'}=\widehat{DAF}=\widehat{FDC}=\widehat{HCB}\)
Lại có: H đối xứng với H' qua BC
\(\Rightarrow\widehat{BCH'}=\widehat{HCB}\)
\(\Rightarrow\widehat{BCH'}=\widehat{BAH'}\Rightarrow\)◊ ABH'C nội tiếp
b . Lấy A' đối xứng với A qua BC
\(\Rightarrow BC\perp AA'\Rightarrow A,H,D,H',A'\) thẳng hàng
Vì \(H,H'\) đối xứng qua BC , A,A' đối xứng qua BC
\(\Rightarrow\widehat{BHC}=\widehat{BH'C},\widehat{BAC}=\widehat{BA'C}\)
Lại có ◊ ABH'C nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{BH'C}=180^0\)
\(\Rightarrow\widehat{BA'C}+\widehat{BHC}=180^0\)
=> ◊ BHCA' nội tiếp
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp \(\Delta A'BC\)
Ta có : A , A' đối cứng qua BC
\(\Rightarrow A'B=AB,CA=CA'\Rightarrow\Delta ABC=\Delta A'BC\left(c.c.c\right)\)
=> Bán kính đường tròn ngoại tiếp \(\Delta A'BC\) bằng bán kính đường tròn ngoại tiếp ΔABC
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp ΔABC