Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

A B C I K H D M O N
a, C thuộc đường tròn đk AD (gt) => ^ACD = 90 => AC _|_ CD mà có BH _|_ AC => CD // BH
B thuộc đường tròn đk AD (gt) => ^ABD = 90 => AB _|_ BD mà có CH _|_ AB => BD // CH
=> BHCD là hình bình hành
b, có BHCD là hình bình hành => M là trung điểm của HD
Có O là trung điểm của AD do AD là đường kính
=> MO là đường trung bình của tam giác AHD
=> MO = 1/2AH
=> AH = 2MO
c, Gọi AM cắt HO tại N
=> N là trọng tâm của tam giác AHD
=> AN = 2/3AM
mà có AM là đường trung tuyến của tam giác ABC
=> H là trọng tâm của tam giác ABC
ờm câu c cũng không chắc lắm

ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)

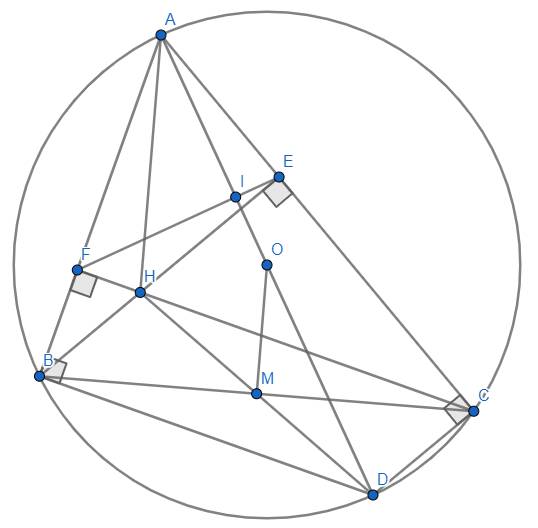
a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).
Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).
Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).
b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)
Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)
Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.
Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.
c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)
Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).
Và : \(BE\perp AC\left(gt\right)\)
Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.
Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)
Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).
Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).
d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).
Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).
Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)
Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)
Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)
\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)
\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)
\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)
\(\Rightarrow OA\perp EF\) (đpcm).