Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Nếu AB = AC:
Xét tam giác ABN và tam giác ACM có:
AN = AM (gt)
AB = AC (gt)
Góc A chung
\(\Rightarrow\Delta ABN=\Delta ACM\left(c-g-c\right)\)
\(\Rightarrow BN=CM\) (Hai cạnh tương ứng)
2.
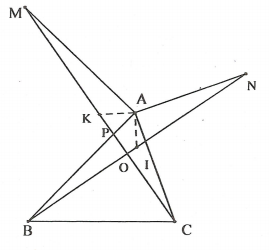
a) Trên cạnh AB lấy điểm M' sao cho AM' = AC.
Ta có ngay \(\Delta AM'N=\Delta ACM\left(c-g-c\right)\)
\(\Rightarrow MC=NM'\)
Lại có AM' < AB nên NM' < NB
Vậy nên BN > CM
b) Ta thấy ngay MK > KN mà BN > MC nên BK = BN - KN > KC = MC - MK

Xét ΔABCΔABC có :
AB=ACAB=AC ( gt )
⇒ΔABC⇒ΔABC cân tại AˆA^
⇒Bˆ=Cˆ⇒B^=C^
Ta có : AB=AC⇒12AB=12AC⇒BM=CNAB=AC⇒12AB=12AC⇒BM=CN
Xét ΔBNCΔBNC và ΔCMBΔCMB có :
CN=BM(cmt)CN=BM(cmt)
Bˆ=Cˆ(cmt)B^=C^(cmt)
ACAC là cạnh chung
Do đó 2 tam giác bằng nhau.
Vậy ...................
LINK MÌNH NHA

3b)
Ta có tg BNK vuông tại K ->BN>BK
Ta có IK=MN(tính chất đoạn chắn)
Ta có : BC+MN=BK+KC+MN=BK+BI+IK=2BK
Vì BK<BN->2BK<2BN->BN>BK/2->BN>BC+MN/2

A B C M N H P Q
Xét tam giác ABN và tam giác ACM có
\(\hept{\begin{cases}AB=AC\\AM=AN\left(\frac{1}{3}AB=\frac{1}{3}AC\right)\\\widehat{A}\text{ chung}\end{cases}}\Rightarrow\Delta ABN=\Delta ACM\left(\text{c.g.c}\right)\)
=> BN = CM (cạnh tương ứng)
=> \(\widehat{ABN}=\widehat{ACM}\)(cạnh tương ứng)
b) Vì \(\hept{\begin{cases}\widehat{ABC}=\widehat{ACB}\left(\Delta ABC\text{ cân}\right)\\\widehat{ABN}=\widehat{ACM}\left(cmt\right)\end{cases}}\Rightarrow\widehat{ABC}-\widehat{ABN}=\widehat{ACB}-\widehat{ACM}\)
=> \(\widehat{NBC}=\widehat{MCB}\text{ hay }\widehat{HBC}=\widehat{HCB}\Rightarrow\Delta HBC\text{ cân tại H }\left(ĐPCM\right)\)
=> HB = HC
c) Qua H kẻ đường thẳng PQ // BC (Q \(\in AC;P\in AB\))
Vì PQ//BC
=> \(\hept{\begin{cases}\widehat{APQ}=\widehat{ABC}\left(\text{đồng vị}\right)\\\widehat{AQP}=\widehat{ACB}\left(\text{ đồng vị}\right)\end{cases}}\text{mà }\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{APQ}=\widehat{AQP}\)
=> Tam giác APQ cân tại A
=> AP = AQ
=> PB = QC
Xét tam giác PBH và tam giác QCH có :
\(\hept{\begin{cases}PB=QC\left(cmt\right)\\HB=HC\left(\text{câu b}\right)\\\widehat{PBH}=\widehat{QCH}\left(\Leftrightarrow\widehat{ABN}=\widehat{ACM}\left(\text{câu a}\right)\right)\end{cases}\Rightarrow\Delta PBH}=\Delta QCH\left(c.g.c\right)\)
=> PH = QH (cạnh tương ứng)
Xét tam giác APH và tam giác AQH có :
\(\hept{\begin{cases}AP=AQ\\PH=QH\\AH\text{ chung}\end{cases}}\Rightarrow\Delta APH=\Delta AQH\left(c.c.c\right)\)
=> \(\widehat{AHP}=\widehat{AHQ}\left(\text{cạnh tương ứng}\right)\text{ mà }\widehat{AHP}+\widehat{AHQ}=180^{\text{o}}\Rightarrow\widehat{AHP}=\widehat{AHQ}=90^{\text{o}}\Rightarrow AH\perp PQ\)
Lại có PQ//BC
=> AH \(\perp\)BC (đpcm)