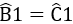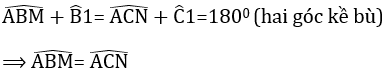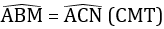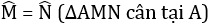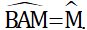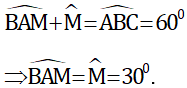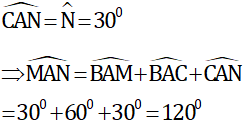Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
góc BAM chung
=>ΔABM đồng dạng với ΔACN
=>AM/AN=AB/AC
=>AM*AC=AN*AB và AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc MAN chung
=>ΔAMN đòng dạng với ΔABC
c: ΔAMN đồng dạng với ΔABC
=>S AMN/S ABC=(AM/AB)^2=(cos60)^2=1/4
=>S ABC=4*S AMN

a) Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{BAM}\) chung
Do đó: ΔAMB\(\sim\)ΔANC(g-g)
Suy ra: \(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Xét ΔAMN và ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)(cmt)
\(\widehat{NAM}\) chung
Do đó: ΔAMN\(\sim\)ΔABC(c-g-c)

a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)

a: XétΔAMB vuông tại M và ΔANC vuông tại N có
góc A chung
Do đó: ΔAMB\(\sim\)ΔANC
b: Ta có: ΔANH vuông tại N
mà NI là đường trung tuyến
nên NI=AH/2(1)
Ta có: ΔAMH vuông tại M
mà MI là đường trung tuyến
nên MI=AH/2(2)
Từ (1) và (2) suy ra NI=MI(3)
Ta có: ΔNBC vuông tại N
mà NK là đường trung tuyến
nên NK=BC/2(4)
Ta có: ΔMBC vuông tại M
mà MK là đường trung tuyến
nên MK=BC/2(5)
Từ (4), (5) suy ra NK=MK(6)
Từ (3) và (6) suy ra IK là đường trung trực của MN

a: Xet ΔAMB vuông tại M và ΔANC vuông tại N có
góc MAB chung
=>ΔAMB đồng dạng với ΔANC
=>AM/AN=AB/AC
=>AM*AC=AN*AB; AM/AB=AN/AC
b: Xet ΔAMN và ΔABC co
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
c: góc MPH=góc ACN
góc NPH=góc ABM
góc ACN=góc ABM
=>góc MPH=góc NPH
=>PH là phân giác củagóc MPN

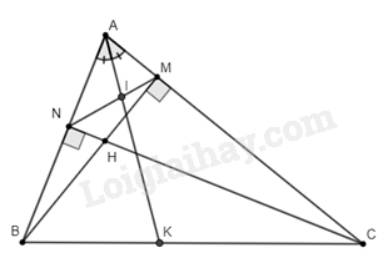
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).

a) ΔABC cân tại A suy ra
Ta lại có :
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai góc tương ứng) ⇒ ΔAMN cân tại A.
b) Hai tam giác vuông BHM và CKN có
BM = CN (gt)
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Theo câu b ta có ΔBHM = ΔCKN ⇒HM = KN (hai góc tương ứng)
Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.
d) ΔBHM = ΔCKN
Vậy tam giác OBC là tam giác cân tại O.
e) Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒
Mà theo tính chất góc ngoài trong ΔBAM thì
Tương tự ta có
Tam giác cân OBC có góc B3=60º nên ΔOBC là tam giác đều.
a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=1800−12002=6002=3001800−12002=6002=300
vậy góc AMN=30độ