Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(BH\perp AD\left(gt\right)\Rightarrow\widehat{BHA}=\widehat{BHD}=90^0\)
\(CK\perp AD\left(gt\right)\Rightarrow\widehat{AKC}=90^0\)
Xét \(\Delta BHD\)và \(\Delta CKD\) có:
\(\widehat{BHD}=\widehat{CKD}=90^0\)
\(\widehat{BDH}=\widehat{CDK}\) (đối đỉnh)
Do đó: \(\Delta BHD\infty\Delta CKD\left(g.g\right)\)
b, Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(\widehat{BAH}=\widehat{CAK}\) (vì AD là tia p/g của góc BAC)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
Do đó: \(\Delta ABH\infty\Delta ACK\left(g.g\right)\)
Suy ra: \(\frac{AB}{AH}=\frac{AC}{AK}\) hay \(AB.AK=AC.AH\)
C, \(\Delta ABH\infty\Delta ACK\left(cmt\right)\Rightarrow\frac{BH}{CK}=\frac{AB}{AC}\left(1\right)\)
\(\Delta BHD=\Delta CKD\left(cmt\right)\Rightarrow\frac{DH}{DK}=\frac{BH}{CK}\left(2\right)\)
Từ (1) và (2), ta được: \(\frac{DH}{DK}=\frac{BH}{CK}=\frac{AB}{AC}\)
d, Gọi giao điểm giữa FM và BH là O và giao điểm giữa FM và CK là I.
Bạn chứng minh được tam giác BOF tại O và tam giác CIE vuông tại I
\(\Delta BOM=\Delta CIM\left(ch.gn\right)\Rightarrow BO=CI\)(2 cạnh tương ứng)
\(AD//FM\left(gt\right)\Rightarrow\hept{\begin{cases}\widehat{BAD}=\widehat{F}\\\widehat{DAC}=\widehat{IEC}\end{cases}}\)(đồng vị)
Suy ra: \(\widehat{F}=\widehat{IEC}\)
Mà \(\hept{\begin{cases}\widehat{F}+\widehat{FBO}=90^0\\\widehat{IEC}+\widehat{ICE}=90^0\end{cases}}\)
Nên \(\widehat{FBO}=\widehat{ICE}\)
Chứng minh được \(\Delta FBO=\Delta ECI\left(g.c.g\right)\Rightarrow BF=CE\)(2 cạnh tương ứng)
Chúc bạn học tốt.

fdsafdsajhbsdkbdkjjdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdfdsafdsajhbsdkbdkjjdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhdbkjdbjhjdbdhdhdhdhdhdhdhdhdhdhdhdhhdhdhd
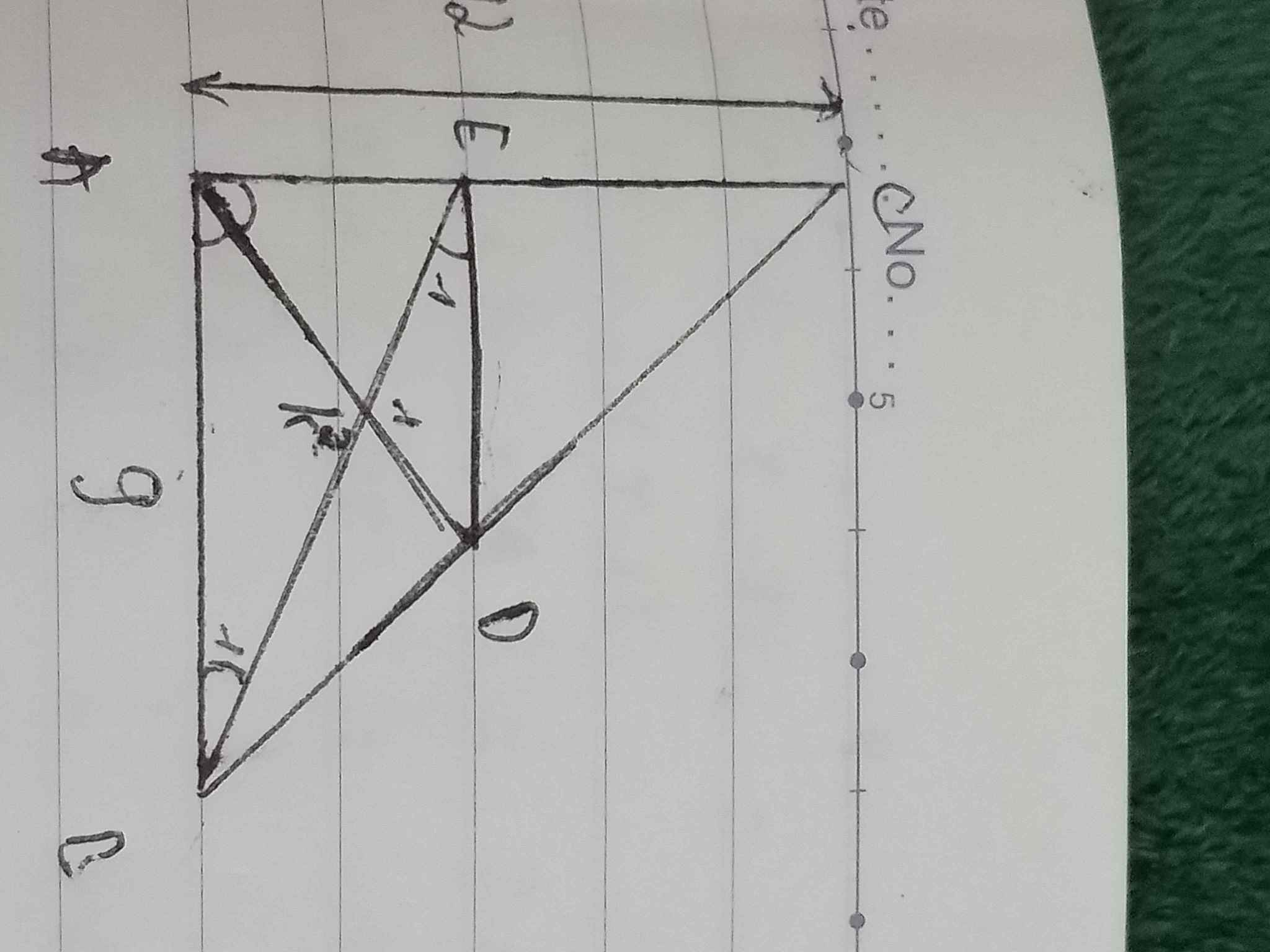


a.
\(\widehat{BED}=\widehat{DAC}\left(so-le-trong\right)\)
Mà \(\widehat{BAD}=\widehat{DAC}\left(gt\right)\)
\(\Rightarrow\widehat{BAE}=\widehat{BEA}\)
Suy ra tam giác ABE cân tại B.
b.
Xét hai tam giác BDE và CDA, ta có:
\(\left\{{}\begin{matrix}\widehat{BDE}=\widehat{CDA}\left(đ^2\right)\\\widehat{BED}=\widehat{DAC}\left(slt\right)\end{matrix}\right.\Rightarrow\Delta BDE\sim\Delta CDA\left(gg\right)\)
\(\Rightarrow\dfrac{BD}{BE}=\dfrac{CD}{CA}\Leftrightarrow\dfrac{BD}{AB}=\dfrac{CD}{AC}\Leftrightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
a, ta có: AC//BE =>góc CAD=DEB( vì hai góc so le trong)
Mà góc BAD=CAD =>DEB=BAD
Vậy tam giác ABE cân tại B(đpcm)