Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Py-ta-go vào tam giác AHB vuông tại H có:
\(AB^2=AH^2+BH^2\)
=>\(BH^2=AB^2-AH^2=\left(8,5\right)^2-4^2=72.25-16=56.25\)
=> \(BH=\sqrt{56,25}=7.5\)
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H có:
\(AC^{2^{ }}=AH^2+HC^2\)
=>\(HC^2=AC^2-AH^2=5^2-4^2=25-16=9\)
=>\(HC=\sqrt{9}=3\)
Vì H thuộc BC => BC=HB+HC=7.5+3=10.5
Chu vi tam giác ABC là: AB+AC+BC=8,5+5+10,5=24(cm)
Vậy chu vi tam giác ABC là 24 cm
Kết quả không phải là 24 cm. Vì H nằm ngoài đoạn thẳng BC.

Áp dụng định lý Pitago, ta có: \(AC^2=AH^2+HC^2\)
\(\Rightarrow20^2=12^2+HC^2\)
\(\Rightarrow HC^2=20^2-12^2\)
\(\Rightarrow HC^2=400-144=256\)
\(\Rightarrow HC=16\left(cm\right)\)
Áp dụng định lý Pitago, ta có: \(AB^2=BH^2+AH^2\)
\(\Rightarrow AB^2=5^2+12^2\)
\(\Rightarrow AB^2=25+144=169\)
\(\Rightarrow AB=13\left(cm\right)\)
Vậy CV tam giác ABC là
\(20+5+16+13=54\left(cm\right)\)

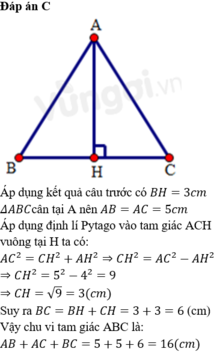
Ta có:\(AC^2=HC^2+AH^2\)(Định lý pytago)
\(\Rightarrow AH^2=AC^2-HC^2=4^2-2^2=16-4=12\)
\(\Rightarrow AH=\sqrt{12}\approx3\)
Độ dài BC là :3+2=5
Chu vi của tam giác ABC la:\(4+5+5\approx14\)

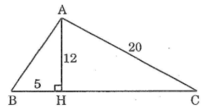
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

Hình bạn tự vẽ nhé
AH vuông góc với BC => Tam giác AHB và tam giác AHC vuông tại H
Áp dụng định lí Pytago cho tam giác vuông AHB ta được :
AB2 = AH2 + BH2
BH = \(\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3cm\)
Áp dụng định lí Pytago cho tam giác vuông AHC ta được :
AC2 = AH2 + HC2
\(AC=\sqrt{AH^2+HC^2}=\sqrt{4^2+12^2}=12,649...\approx12,65cm\)
H thuộc BC => BC = BH + HC = 3 + 12 = 15cm
Chu vi hình tam giác ABC = AB + AC + BC = 5 + 12, 65 + 15 = 32, 65cm
#Sai thì bỏ qua nhé xD
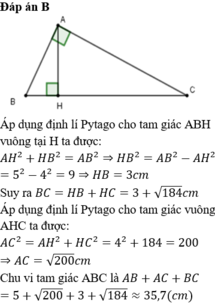
AD định lý Pytago vào trong tam giác ABH vuông tại H ta có: BH2 = AB2 - AH2=25-16=9
Suy ra BH=3(cm)
Ta có BC=BH+CH =12+3=15(cm)
AD định lý Pytago vào trong tam giác AHC vuông tại H ta có:AC2=AH2+HC2=42+122=160
Suy ra:AC=12,65(cm;tương đương)
Vậy chu vi tam giác ABC là: 5+15+12.65=32.65(cm)
Gọi I là giao điểm của AH và BC
Áp dụng định lí pytago trong tam giác vuông ABI ta có
BI2=AB2-AH2
BI2=8.52-42=56.25
BI=căn bậc hai của 56.25
Áp dụng định lí pytago trong tam giác vuông AIC ta có
IC^2=AC^2-AI^2
HC^2=5^2-4^2=9
HI=3
Ta co BI+IC=BC
7.5+3=10.5
Chu vi của tam giác ABC là 8.5+5+10.5=24