Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(X\text{ét}\Delta BDM\)có \(\widehat{BMD}+\widehat{BDM}+\widehat{DMB=180}\)
\(\Leftrightarrow\widehat{BMD}+90+60=180\)
\(\Rightarrow\widehat{BMD}=30\)
Tương tự vs tg EMC có EMC=30
\(X\text{ét}\widehat{DME}=180-\left(\widehat{BMD}+\widehat{EMC}\right)=180-30-30=120\)

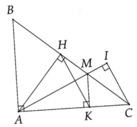
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAIH vuông tại H và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Ta có: AI=AK
nên A nằm trên đường trung trực của IK(1)
ta có: MI=MK
nên M nằm trên đường trung trực của IK(2)
ta có: HI=HK
nên H nằm trên đường trung trực của IK(3)
Từ (1), (2) và (3)suy ra A,M,H thẳng hàng

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAIH vuông tại H và ΔAKH vuông tại K có
AH chung
\(\widehat{IAH}=\widehat{KAH}\)
Do đó: ΔAIH=ΔAKH
Suy ra: AI=AK
c: Ta có: AI=AK
nên A nằm trên đường trung trực của IK(1)
ta có: MI=MK
nên M nằm trên đường trung trực của IK(2)
ta có: HI=HK
nên H nằm trên đường trung trực của IK(3)
Từ (1), (2) và (3)suy ra A,M,H thẳng hàng