Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

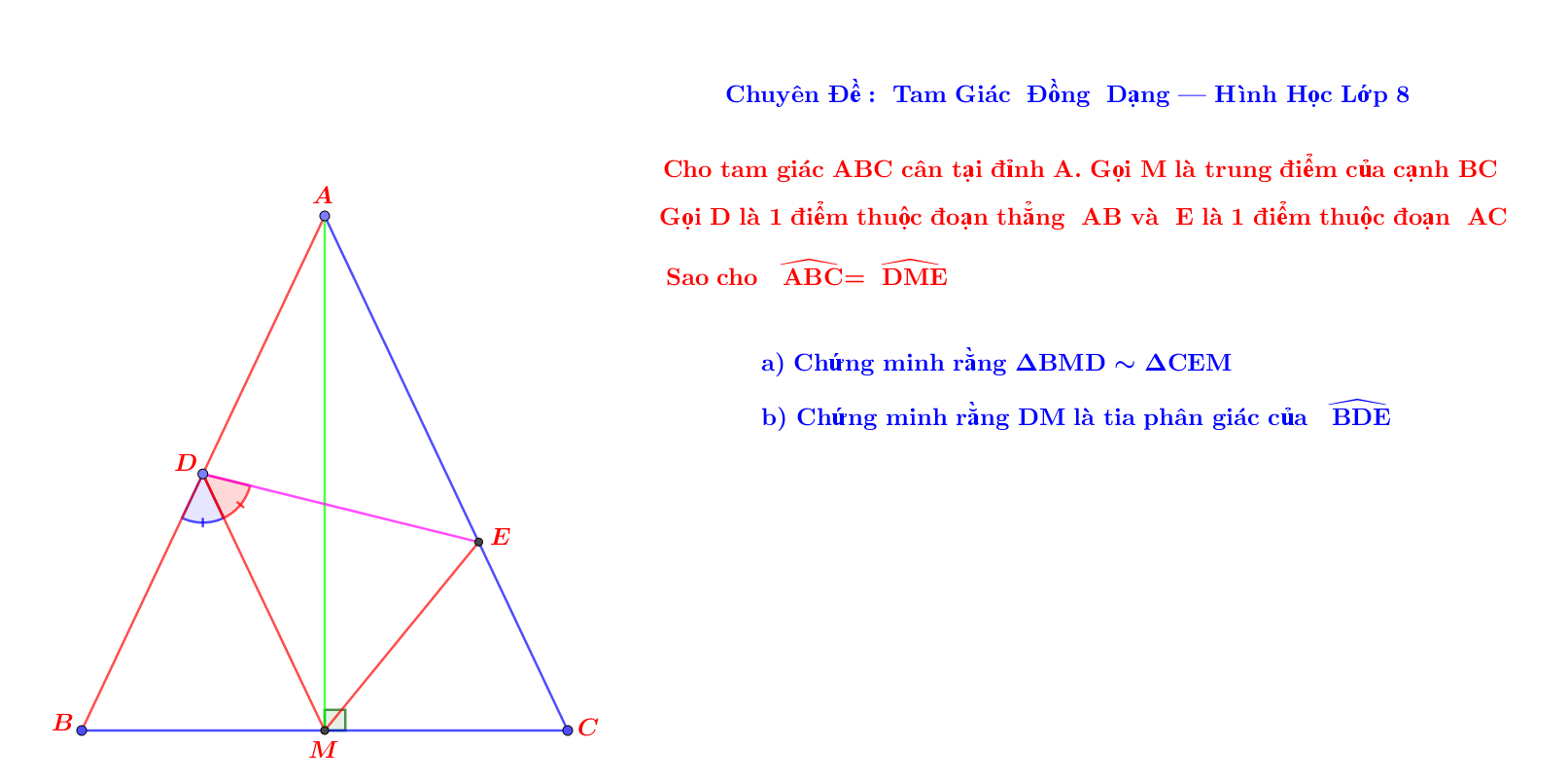
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.

B K E C H A D M
a)DC//BE (cùng vuông góc với AC);DB//CE (cùng vuông góc với AB) => là hình bình hành
b) hình bình hình thì 2 đường chéo giao nhau tại trung điểm mỗi đường hay DE cắt BC tại M và M là trung điểm DE
Để DE đi qua A tức là D;E;A thằng hàng
mà AE là một đường cao hay AE vuông góc BC nên D;E;A thẳng hàng tức là DE vuông góc với BC
hình bình hành có 2 đường chéo vuông góc là hình thoi
c) tứ giác ABDC có góc DBA +góc DCA =180 nên góc BAC+ góc BDC=180
Mượn hình của bạn Manh nhé!
a) Ta có: DB // CK ( \(\perp\)AB)
=> DB // CE (1)
BH // DC ( \(\perp\) AC )
=> DC // BE (2)
Từ (1) ; (2) => DBEC là hình bình hành.
b) +) Theo câu a) DBEC là hình bình hành
=> Hai đường chéo BC và DE cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm BC => M là trung điểm DE.
+) CK; BH là hai đường cao của \(\Delta ABC\) và CK ; BH cắt nhau tại E.
=> E là trực tâm của \(\Delta ABC\)
=> AE là đường cao hạ từ A. (3)
Theo giả thiết DE qua A mà DE cắt BC tại M là trung điểm cạnh BC
=> AE qua trung điểm của cạnh BC
=> AE là đường trung tuyến của \(\Delta ABC\) (4)
Từ (3); (4) => \(\Delta ABC\) cân tại A
c) Em tham khảo bài làm bạn Manh.