Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

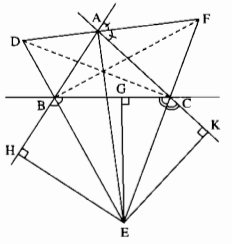
a) E thuộc tia phân giác của \(\widehat{CBH}\)
\(\Rightarrow\)EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của \(\widehat{BCK}\)
\(\Rightarrow\)EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
\(\Rightarrow\)E thuộc tia phân giác của \(\widehat{BAC}\)mà E khác A
Vậy AE là tia phân giác của \(\widehat{BAC}\)
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
\(\Rightarrow AE\perp AF\) (tính chất hai góc kề bù)
Hay \(AE\perp DF\)
d) Chứng minh tương tự câu a ta có BF là tia phân giác của \(\widehat{ABC}\)
CD là tia phân giác của \(\widehat{ACB}\)
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
\(\Rightarrow BF\perp BE\) (tính chất hai góc kề bù)
Hay \(BF\perp ED\)
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
\(\Rightarrow CD\perp CE\)(tính chất hai góc kề bù)
Hay \(CD\perp EF\)
Các đường thẳng AE, FB, DC là các đường cao trong tam giác DEF.

mình chỉ lm dc câu a thôi
đặt ABx là góc ngoài tam giác ABC ( thêm x vào, dòng này ko ghi vào vở)
a)vì AD là tia phân giác của góc A, CE là tia phân giác góc C nên
BO là tia phân giác góc B
=> góc ABO = 1/2 góc ABC (1)
vì BF là tia phân giác góc B nên:
góc FBA = 1/2 góc ABx (2)
cộng vế 1 và 2 vào ta có
góc ABO + góc FBA = 1/2 ( góc ABC + góc ABx)
góc FBO =1/2 * 180 độ
góc FBO = 90 độ
=> vuông

â)xét tam giác AMBvà tam giác AMC
AB=AC( gt)
AM chung
MB=MC ( M là trung điểm của BC )
=> tam giác AMB= tam giác AMC ( c.c.c)
=> góc AMB= góc AMC ( 2 góc tương ứng )
mà góc AMB+ góc AMC = 180O ( 2 GÓC KỀ BÙ )
=> góc AMB= góc AMC=90O
=> AM vuông góc với BC
b) xét tam giác ADF và tam giác ADE
DF=DE ( gt)
góc ADF= góc CDE ( 2 góc đối đỉnh )
AD=CD ( D là trung điểm của AC)
=> tam giác ADF = tam giác ADE ( c.g.c)
=> góc CAF= góc ACÊ ( 2 góc tương ứng ) mà chúng ở vị trí so le trong do AC cắt AF và CE
=.> AF// CE


a) E thuộc tia phân giác của ˆCBHCBH^
⇒⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ˆBCKBCK^
⇒⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒⇒ E thuộc tia phân giác của ˆBACBAC^ mà E # A
Vậy AE là tia phân giác của ˆBACBAC^
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒⇒ AE⊥AFAE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DFAE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ˆABCABC^
CD là tia phân giác của ˆACBACB^
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥EDBF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE⇒CD⊥CE (tính chất hai góc kề bù)
Hay CD⊥EF

a) E thuộc tia phân giác của ˆCBHCBHˆ
⇒⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ˆBCKBCKˆ
⇒⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒⇒ E thuộc tia phân giác của ˆBACBACˆ mà E # A
Vậy AE là tia phân giác của ˆBACBACˆ
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒⇒ AE⊥AFAE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DFAE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ˆABCABCˆ
CD là tia phân giác của ˆACBACBˆ
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥EDBF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE⇒CD⊥CE (tính chất hai góc kề bù)
Hay CD⊥EF