Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

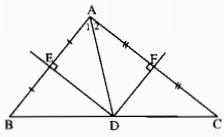
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC

Vì AC là đường trung trực của BB' nên CB=CB'
=>ΔCBB' cân tại C
hay \(\widehat{BCA}=\widehat{B'CA}\)
Vì AB là đường trung trực của CC' nên BC=BC'
=>ΔBCC' cân tại B
hay \(\widehat{CBA}=\widehat{C'BA}\)
Vì AB và AC lần lượt là các đường phân giác của các góc CBB' và BCB'
và AB cắt AC tại A
nên A là điểm cách đều ba cạnh của ΔA'BC

Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.

Tự vẽ hình nha ^^
a, Ta có: tam giác ABC cân tại A có AO là đường trung trực (gt)
=> AO cũng là phân giác của góc BAC
=> góc OAB = góc OAC (1)
Gọi OD là đường trung trực của AC
Xét tam giác AOC có OD vừa là đường cao vừa là trung tuyến => AOC cân tại O
=> góc OAC = góc OCA (2)
Từ (1), (2) => đpcm
b, Theo câu a: tam giác AOC cân tại O
=> OA = OC (3)
Và MA = CN (gt) (4)
Mặt khác: góc MAC = góc ABC + góc ACB (góc ngoài)
=> góc MAO = góc MAC + góc OAC = góc ABC + góc ACB + góc OAC (*)
Góc BCN = góc BAC + góc ABC (góc ngoài)
=> góc OCN = góc BCN + góc OCB = góc BAC + góc ABC + góc ACB - góc OCA
<=> góc OCN = góc ABC + góc ACB + (góc BAC - góc OAB) (góc OAB = góc OCA théo câu a)
<=> góc OCN = góc ABC + góc ACB + góc OAC (**)
Từ (*), (**) => góc MAO = góc OCN (5)
Từ (3), (4), (5) => tam giác OAM = tam giác OCN (c-g-c)

+) Xét tam giác ADE và BDE có:
DE chung
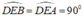
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
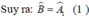
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
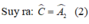
Từ (1) và (2) suy ra: 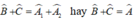
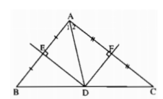
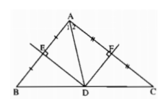
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).