Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BC=\sqrt{3^2+4^2}=5\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{12}{5}cm\)
\(AD=\sqrt{bc\left(1-\left(1-\dfrac{a}{b+C}\right)^2\right)}=\dfrac{4\sqrt{3}}{7}\)

1/2*sin(60)*6*10=Sabc=S abd+S acd=1/2*sin(30)*6*AD+1/2*sin(30)*10*AD
giải pt
oOo KHÙNG oOo đây chắc là minh triều nek!!!
46465475457

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
b: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
c:
Sửa đề: AP là phân giác của góc BAC
Xét tứ giác AEPF có
\(\widehat{AEP}=\widehat{AFP}=\widehat{FAE}=90^0\)
=>AEPF là hình chữ nhật
Hình chữ nhật AEPF có AP là phân giác của góc FAE
nên AEPF là hình vuông

a: Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=13^2-5^2=144\)
hay AC=12(cm)

a, vi D nam giua cung BC =>cung BD = cung CD=>goc BAD = goc CAD
=>AD la phan giac cua goc BAC
b, vi D la diem chinh giua cua cung BC =>OD vuong goc vs BC
=>tam giac BOD vuong tai O
=>BD2=OB2+OD2=R2+R2=2R=>BD=R căn 2

a: AE là phân giác của góc BAC
=>EB=EC
mà OB=OC
nên OE là trung trực của BC
=>OE vuông góc BC
=>OE//AH
b: Điểm M ở đâu vậy bạn?
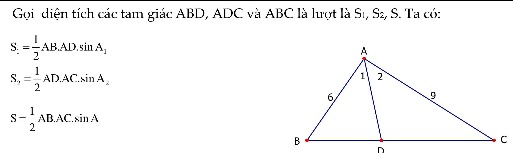
cho tam giác ABC vs đường phân giác trong của gócBAC là AD bt AB-6 AC=9 cà góc A=68 .Tính độ dài AD