Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

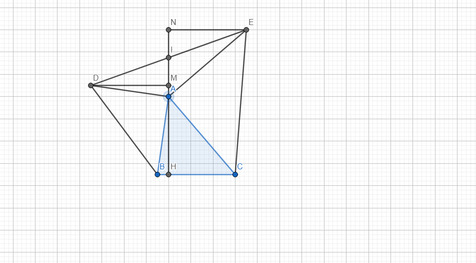
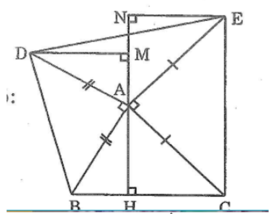
Cho t/giác ABC , kẻ AH vuông BC . Ở phía ngoài t/giác ABC vẽ các tam giác vuông cân tại A là t/giác ABD và t/giác ACE . Kẻ DM , EN vuông với AH . Chứng minh DM = EN

Ta có: ∠(BAH) +∠(BAD) +∠(DAM) =180o(kề bù)
Mà ∠(BAD) =90o⇒∠(BAH) +∠(DAM) =90o(1)
Trong tam giác vuông AMD, ta có:
∠(AMD) =90o⇒∠(DAM) +∠(ADM) =90o(2)
Từ (1) và (2) suy ra: ∠(BAH) =∠(ADM)
Xét hai tam giác vuông AMD và BHA, ta có:
∠(BAH) =∠(ADM)
AB = AD (gt)
Suy ra: ΔAMD= ΔBHA(cạnh huyền, góc nhọn)
Vậy: AH = DM (hai cạnh tương ứng) (3)

D B C E N M A H
a, có góc ADM+DAM=90độ
có góc DAM+DAB+BAH=90độ
=>DAM+BAH=90 độ=>BAH=ADM
có DAM+ADM=90 độ
có BAH+ABH=90 độ
mà ADM=BAH=>ABH=DAM
xét tg DAM và tg BAH
AB=AD
góc ADM=BAH => tg DAM=tg ABH(g.c.g)
góc DAM=ABH
=> DM=AH(2 cạnh t/ứ)
b, nối D,E
xét tg NEA và tg AHC giống ý a, rùi có NE=AH mà DM=AH => DM=NE
gọi giao điểm của DE và NA là T => NTE=DTM(đối đỉnh)
Xét tg MDT và tg NET
NE=DM
NET=TDM(2 góc kia = nhau thì góc này =) => tgMTD=tgNET(g.c.g)
ENT=DMT(=90 độ)
=> DT=ET(2 cạnh t.ứ)=> MN đi qua trung điểm của DE
c, có EAC=DAB(=90độ)=> EAC+BAC=DAB+BAC(1)
DA=BA(2), CA=EA(3)
từ 1,2 3 => 2 tg đó = nhau

Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE

a)- Ta có: △ABD vuông tại A và \(AB=AD\left(gt\right)\)
=>△ABD vuông cân tại A.
- Ta có: \(\left[{}\begin{matrix}DM\perp AH\left(gt\right)\\BC\perp AH\left(gt\right)\end{matrix}\right.\)=>\(DM\)//\(BC\).
=>\(\widehat{BDM}+\widehat{DMH}=180^0\) (2 góc trong cùng phía).
=>\(\widehat{ADM}+\widehat{ADB}+\widehat{ABH}+\widehat{ABD}=180^0\).
Mà \(\widehat{ADB}=\widehat{ABD}=45^0\)(△ABD vuông cân tại A)
=>\(\widehat{ADM}+45^0+\widehat{ABH}+45^0=180^0\)
=>\(\widehat{ADM}+\widehat{ABH}+90^0=180^0\)
=>\(\widehat{ADM}+\widehat{ABH}=90^0\)
Mà \(\widehat{ADM}+\widehat{MAD}=90^0\) (△ADM vuông tại M).
=>\(\widehat{ABH}=\widehat{MAD}\).
- Xét △ADM vuông tại M và △BAH vuông tại H có:
\(AD=AB\left(gt\right)\)
\(\widehat{ABH}=\widehat{MAD}\) (cmt)
=>△ADM = △BAH (cạnh huyền-góc nhọn).
=>\(DM=AH\) (2 cạnh tương ứng).
b) - Sửa đề: Gọi I là trung điểm của MN.
- Ta có: △ACE vuông tại A và \(AC=AE\left(gt\right)\)
=>△ACE vuông cân tại A.
- Ta có: \(\left[{}\begin{matrix}EN\perp AH\left(gt\right)\\BC\perp AH\left(gt\right)\end{matrix}\right.\)=>\(EN\)//\(BC\).
=>\(\widehat{NEC}+\widehat{HCE}=180^0\) (2 góc trong cùng phía).
=>\(\widehat{AEN}+\widehat{AEC}+\widehat{ACE}+\widehat{ACB}=180^0\).
Mà \(\widehat{AEC}=\widehat{ACE}=45^0\)(△ACE vuông cân tại A)
=>\(\widehat{AEN}+45^0+\widehat{ACB}+45^0=180^0\)
=>\(\widehat{AEN}+\widehat{ACB}+90^0=180^0\)
=>\(\widehat{AEN}+\widehat{ACB}=90^0\)
Mà \(\widehat{AEN}+\widehat{NAE}=90^0\) (△ANE vuông tại N).
=>\(\widehat{ACB}=\widehat{NAE}\).
- Xét △ANE vuông tại N và △CHA vuông tại H có:
\(AN=AC\left(gt\right)\)
\(\widehat{ACB}=\widehat{NAE}\) (cmt)
=>△ANE = △CHA (cạnh huyền-góc nhọn).
=>\(NE=AH\) (2 cạnh tương ứng) mà \(DM=AH\) (cmt)
=>\(NE=DM\).
- Xét △DMI và △ENI có:
\(\left[{}\begin{matrix}DM=NE\left(cmt\right)\\\widehat{DMI}=\widehat{ENI}=90^0\\MI=NI\left(IlàtrungđiểmMN\right)\end{matrix}\right.\)
=>△DMI = △ENI (c-g-c).
=>\(\widehat{DIM}=\widehat{EIN}\) (2 góc tương ứng).
Mà \(\widehat{DIM}+\widehat{DIN}=180^0\) (kề bù).
=>\(\widehat{EIN}+\widehat{DIN}=180^0\)
=>\(\widehat{EID}=180^0\) hay 3 điểm E,I,D thẳng hàng.