Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

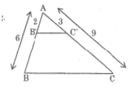
* Cách dựng:
- Trên cạnh AB dựng điểm B' sao cho = 2 cm
- Trên cạnh AC dựng điểm C' sao cho AC' = 3cm
- Nối B'C'
Khi đó AB'C' là tam giác cần dựng
* Chứng minh:
Theo cách dựng, ta có:
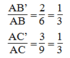
Suy ra: 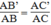
Lại có: ∠ A chung
Vậy △ AB'C' đồng dạng △ ABC (c.g.c)

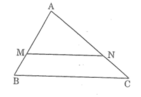
* Cách dựng:
- Trên cạnh AB dựng điểm M sao cho AM = 2/3 AB
- Trên cạnh AC dựng điểm N sao cho AN = 2/3 AC
- Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3
* Chứng minh:
Theo cách dựng ta có:
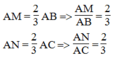
Suy ra: 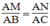
Trong ΔABC, ta có: 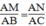
Theo định lí đảo của định lí Ta-lét ta có: MN // BC
Vậy
△
AMN đồng dạng
△
ABC và 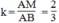

a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).


Có thể dựng được 3 tam giác như vậy