Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì
△
A'B'C' đồng dạng
△
ABC nên 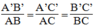
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB + 10,8cm = 16,2 + 10,8 = 27 (cm)
Ta có: 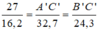
Suy ra: 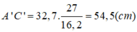
Suy ra: 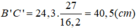

Vì
△
A'B'C' đồng dạng
△
ABC nên 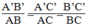
Mà AB = 16,2 cm; BC = 24,3 cm; AC = 32,7 cm nên:
A'B'= AB - 5,4 = 16,2 - 5,4 =10,8 (cm)
Ta có: 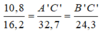
Suy ra: A'C' = (10,8 . 32,7): 16,2 = 21,8 (cm)
B'C'= (10,8 . 24,3): 16,2 = 16,2 (cm)

ΔABC đồng dạng với ΔA'B'C'
=>A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/162=B'C'/243=A'C'/327
=>A'B'/54=B'C'/81=A'C'/109

Ta có
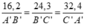
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm

+) Trong tam giác vuông A’B’C’ có \(\widehat{A'}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
A′B′2+A′C′2 =B′C′2
=> A′C′2=B′C′2−A′B′2=152−92=144
=> A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat{A}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
BC2=AB2+AC2= 62+82=100
Suy ra: BC = 10 (cm)
Ta có: \(\dfrac{A'B'}{AB}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(\dfrac{A'C'}{AC}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{B'C'}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
Suy ra: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}=\dfrac{3}{2}\)
Vậy ∆ A’B’C’ đồng dạng với ∆ ABC

TA CÓ AH : AB = A'H' : A'B' => TAM GIÁC AHB ĐỒNG DẠNG TAM GIÁC A'H'B' ( CẠNH HUYỀN - CẠNH GÓC VUÔNG )
=> GÓC B = GÓC B'
TA CÓ AH : AC = A'H' :A'C' => TAM GIÁC AHC ĐỒNG DẠNG TAM GIÁC A'H'C' ( CẠNH HUYỀN - CẠNH GÓC VUÔNG )
=> GÓC C = GÓC C'
- XÉT TAM GIÁC ABC VÀ TAM GIÁC A'B'C' CÓ :
GÓC B = GÓC B' ( CHỨNG MINH TRÊN )
GÓC C = GÓC C' (CHỨNG MINH TRÊN )
=> TAM GIÁC ABC ĐỒNG DẠNG TAM GIÁC A'B'C' (G-G)
