Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì tam giác ABC đồng dạng với tam giác A'B'C' =>AB/A'B'=BC/B'C'=AC/A'C'
=>BC/B'C'=6/8=3/4=>BC=3.10/4=15/2(cm)
ta lại có AC/A'C'=3/4
=>A'C'/4=AC/3=3/1=3
=>AC=9cm=>A'C'=12(cm)
Vậy BC=15/2 cm ,AC=9cm,A'C'=12cm

TA CÓ AH : AB = A'H' : A'B' => TAM GIÁC AHB ĐỒNG DẠNG TAM GIÁC A'H'B' ( CẠNH HUYỀN - CẠNH GÓC VUÔNG )
=> GÓC B = GÓC B'
TA CÓ AH : AC = A'H' :A'C' => TAM GIÁC AHC ĐỒNG DẠNG TAM GIÁC A'H'C' ( CẠNH HUYỀN - CẠNH GÓC VUÔNG )
=> GÓC C = GÓC C'
- XÉT TAM GIÁC ABC VÀ TAM GIÁC A'B'C' CÓ :
GÓC B = GÓC B' ( CHỨNG MINH TRÊN )
GÓC C = GÓC C' (CHỨNG MINH TRÊN )
=> TAM GIÁC ABC ĐỒNG DẠNG TAM GIÁC A'B'C' (G-G)

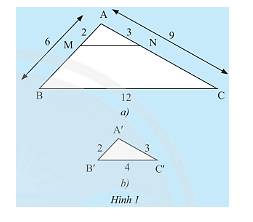
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).

Ta có: ABC đồng dạng với tam giác A'B'C' nên ta có:
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{1}{3}\)(vì \(\frac{AB}{A'B'}=\frac{2}{6}=\frac{1}{3}\)nên 1/3 là tỉ số đồng dạng
hay \(\frac{AC}{A'C'}=\frac{1}{3}\Leftrightarrow\)\(\frac{4}{A'C'}=\frac{1}{3}\Rightarrow A'C'=\frac{4.3}{1}=12\left(cm\right)\)
vậy .....................