Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét tam giác ADN có
B là trung điểm AD(do BA=BD)
N là trung điểm AK (gt)
=> BN là đường trung bình tam giác ADN=> BN =DK/2
b) Xét tam giác BNC có
BN//MK (vì BN//DK)
M là trung điểm BC (gt)
=> K là trung điểm NC
=>KC=NK=1/2AK (vì N là trung điểm AK)
=> KC=1/2Ak hay AK=2KC

b) Từ \(B\) kẻ \(BN//DK\left(N\in AC\right)\)
Xét \(\Delta BNC\) có:
\(BN//MK\left(BN//DK\right)\)
\(BM=MC\left(gt\right)\)
\(\Rightarrow NK=KC\left(1\right)\)
Xét \(\Delta ADK\) có:
\(BN//DK\) ( cách dựng )
\(AB=BD\left(gt\right)\)
\(\Rightarrow AN=NK\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow AN=NK=KC\)
\(\Rightarrow AK=2KC\)
Vậy \(AK=2KC\)


Gọi H là trung điểm của AK
=>BH là đtb của tam giác ADK
=> BH//MK
mà M là trung điểm của BC
=>HK=KC
=> AH=HK=KC
=> AK=2KC

Gọi E là trung điểm của DK
Ta có: BE là đường trung bình của tam giác ADK
\(\Leftrightarrow BE=\frac{1}{2}AK\)(1)
Và BE\\AK
Suy ra: \(\widehat{EBM}=\widehat{C}\)(so le trong)
Chứng minh tam giác BME=tam giác CMK (tự CM)
Suy ra: BE=CK(2)
Từ (1) và (2)
Suy ra: \(CK=\frac{1}{2}AK\Leftrightarrow AK=2KC\)
Vậy....

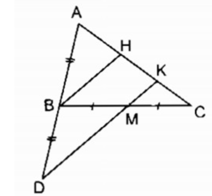
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)
