Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tu ve hinh :
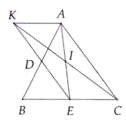
xet tamgiac KDA va tamgiac EDB co : DK = DE (gt)
DB = DA do D la trung diem cua AB (gt)
goc KDA = goc BDE (doi dinh)
=> tamgiac KDA = tamgiac EDB (c - g - c)
=> goc KAD = goc DBE (dn) ma 2 goc nay so le trong
=> KA // BC (dh) (1)
b, (1) => goc KAE = goc AEC (soletrong)
xet tamgiac KAI va tamgiac CEI co : goc KIA = goc EIC (doi dinh)
AI = IE do I la trung diem cua AE (gt)
=> tamgiac KAI = tamgiac CEI (g - c - g)
=> KI = IC (dn) ma I nam giua K va C
=> I la trung diem cua KC (dn)
vay_


a) Xét \(\Delta ADK\)và \(\Delta BDE\)có:
AD = BD (gt)
\(\widehat{ADK}=\widehat{BDE}\)
DK = DE (gt)
Suy ra \(\Delta ADK\)\(=\Delta BDE\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAK}=\widehat{DBE}\)(hai góc tương ứng) và AK = BE
Mà 2 góc này ở vị trí so le trong nên \(AK//BC\)(đpcm)
b) Xét \(\Delta EIC\)và \(\Delta AIK\)có:
EI = AI (gt)
\(\widehat{IEC}=\widehat{IAK}\)(\(AK//BC\),so le trong)
EC = AK ( Vì AK = BE mà BE = EC)
Suy ra \(\Delta EIC\)\(=\Delta AIK\left(c-g-c\right)\)
\(\Rightarrow KI=CI\)(hai cạnh tương ứng)
Từ đề bài suy ra DE là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE//AC\)
CM tương tự được: \(\Delta KIE=\Delta CIA\)
Sao đó c/m \(KIC=180^0\)rồi suy ra I là trung điểm của KC

a) Xét \(\Delta AMB\)và \(\Delta DMC\)có:
MA = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\)(2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
b) Xét \(\Delta AMC\)và \(\Delta DMB\)có:
MA = MD (gt)
\(\widehat{AMC}=\widehat{DMB}\)(2 góc đối đỉnh)
MC = MB (M là trung điểm của BC)
\(\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ACM}=\widehat{DBM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AC//BD\)
c) Ta có: \(\Delta AMC=\Delta DMB\)(theo b)
=> AC = BD (2 cạnh tương ứng)
Xét \(\Delta DBK\)và \(\Delta ACH\)có:
\(\widehat{BKD}=\widehat{CHA}=90^o\left(gt\right)\)
BD = AC (cmt)
\(\widehat{DBK}=\widehat{ACM}\)(cm b)
\(\Rightarrow\Delta DBK=\Delta ACH\left(CH-GN\right)\)
=> BK = CH (2 cạnh tương ứng)
d) Ta có: \(\Delta AMB=\Delta DMC\)(theo a)
=> AB = CD (2 cạnh tương ứng) (1)
\(\widehat{ABM}=\widehat{DCM}\)(2 góc tương ứng)
Mà 2 góc ở vị trí so le trong => AB // CD (2)
Xét \(\Delta ABI\)và \(\Delta CEI\)có:
AI = CI (I là trung điểm của AC)
\(\widehat{AIB}=\widehat{CIE}\)(2 góc đối đỉnh)
BI = EI (I là trung điểm của BE)
\(\Rightarrow\Delta ABI=\Delta CEI\left(c.g.c\right)\)
\(\Rightarrow AB=CE\)(2 cạnh tương ứng) (3)
\(\widehat{ABI}=\widehat{CEI}\)(2 góc tương ứng)(4)
Mà 2 góc này ở vị trí so le trong
=> AB // CE
Từ (1) và (3) => CD = CE (5)
Từ (2) và (4) => C,D,E thẳng hàng (6)
Từ (5) và (6) => C là trung điểm của DE

sai đầu bài ròi bn êi
sai đầu bài thật đấy