Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
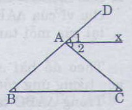
ˆCADCAD^= ˆBB^+ ˆCC^(góc ngoài của tam giác ABC)
= 400+ 400 = 800
ˆA2=12ˆCAD=802=A2^=12CAD^=802=400.
Hai góc so le trong bằng nhau nên Ax// Bc

A B C 1 2 3 P/s : Hình ảnh chỉ có tính chất minh họa cho sản phẩm x
Theo đề ta giải được : \(\widehat{A}=100^0\)
Gọi à là tia phân giác ngoài của góc A .
\(\Rightarrow\widehat{A_2}=\widehat{A_3}=\frac{\left(180^0-100^0\right)}{2}=\frac{80^0}{2}=40^0\)
\(\Rightarrow\widehat{A_2}=\widehat{C}\left(=40^0\right)\)
Mà góc A 1 và góc C là hai góc so le trong .
=> Ax // BC ( đpcm )

A B C x
Tam giác ABC có: góc B +góc C + góc BAC = 180o => 40o + 40o + BAC = 180o => góc BAC = 180o - 80o = 100o
=> góc BAy = 180o - BAC = 180o - 100o = 80o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80o/2 = 40o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40o) Mà hai góc này ở vị trí SLT => Ax // BC
Cho tam giác ABC có B=C=40 độ. Gọi Ax là tia phân giác của góc ngoài ở đỉnh A. Hảy chứng minh Ax//BC


A B C x D M
a, Xét t/g BAM và t/g CAM có:
AB = AC (gt)
MB = MC (gt)
AM : cạnh chung
Do đó t/g BAM = t/g CAM (c.c.c)
b, Vì AB = AC (gt) => t/g ABC cân tại A => góc B = góc C
c, Ta có: góc xAD + góc CAD = góc B + góc C
Mà góc xAD = góc CAD ; góc B = góc C
=> \(2\widehat{CAD}=2\widehat{C}\)
=> góc CAD = góc C
Mà 2 góc này ở vị trí so le trong
=> AD // BC
a,Vì tam giác ABC có AB=AC
=>tam giác ABC cân tại A.
M là trung điểm BC=>BM=MC
Có AM là cạnh chung.
=>tam giác BAM=CAM
b,Do tam giác ABC cân tại A
=>^B=^C

