Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

a) \(\frac{{AM}}{{MB}} = \frac{1}{2}\)
\(\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.
Xét ∆ABC’ với MN // BC’, ta có:
\( \frac{AM}{MB}=\frac{AN}{NC′}\) (định lí Thalès).
Mà theo câu a, \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên ta có \(\frac{{AN}}{{NC}} = \frac{AN}{NC′}\)
Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.
Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.
Vậy đường thẳng d (đi qua M, N) song song với BC.

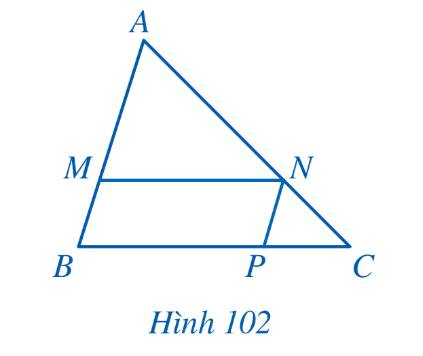
Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).

Vì BMNP là hình bình hành nên \(NP\parallel AB\)\(,\,\,MN = BP,\,\,BM = PN\)
\( \Rightarrow \frac{{NP}}{{AB}} = \frac{{CP}}{{CB}}\) (Định lý Thales)
Ta có: \(\frac{{MN}}{{BC}} = \frac{{BP}}{{BC}}\)
Khi đó: \(\frac{{MN}}{{BC}} + \frac{{NP}}{{AB}} = \frac{{BP}}{{BC}} + \frac{{CP}}{{BC}} = \frac{{BC}}{{BC}} = 1\) (đpcm)

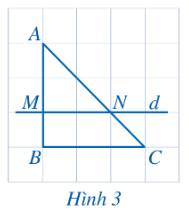
a) Quan sát hình ta thấy \(d\parallel BC\).
b) Ta thấy:
Độ dài AM là 2 lần cạnh của một ô vuông.
Độ dài MB là cạnh của một ô vuông.
\( \Rightarrow \frac{{AM}}{{MB}} = \frac{2}{1} = 2\)
Độ dài AN là 2 lần đường chéo của một ô vuông.
Độ dài NC là độ dài đường chéo của một ô vuông.
\( \Rightarrow \frac{{AN}}{{NC}} = \frac{2}{1} = 2\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).

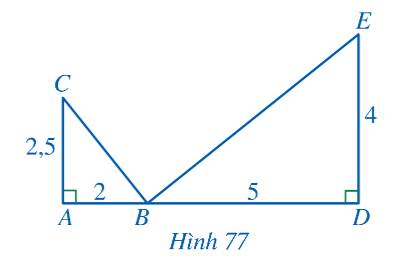
a) Ta thấy \(\frac{{AB}}{{DE}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{AC}}{{DB}} = \frac{2,5}{5} = \frac{1}{2}\)
\( \Rightarrow \frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\)
Xét tam giác ABC và tam giác DEB có:
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DB}}\) và \(\widehat {CAB} = \widehat {BDE} = 90^\circ \)
\( \Rightarrow \Delta ABC \backsim \Delta DEB\) (c-g-c)
\( \Rightarrow \widehat {ABC} = \widehat {BED}\)
b) Vì \(\Delta ABC \backsim \Delta DEB\) nên \(\widehat {ACB} = \widehat {DBE}\)
Mà tam giác ABC vuông tại A nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \) hay \(\widehat {DBE} + \widehat {ABC} = 90^\circ \)
Ta thấy
\(\begin{array}{l}\widehat {DBE} + \widehat {CBE} + \widehat {ABC} = 180^\circ \\ \Rightarrow \widehat {CBE} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {CBE} = 90^\circ \end{array}\)
Vậy \(BC \bot BE\).

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

Vì \(MN\parallel B'C'\) nên \(\widehat {A'MN} = \widehat {A'B'C'}\) (hai góc đồng vị)
\( \Rightarrow \widehat M = \widehat B\)
Xét tam giác A’MN và tam giác ABC có:
\(\widehat {A'} = \widehat A;\,\,A'M = AB;\,\,\widehat M = \widehat B\)
\( \Rightarrow \Delta A'MN = \Delta ABC\) (g-c-g)
Vì \(MN\parallel B'C'\) nên \(\Delta A'MN \backsim \Delta A'BC\)
\( \Rightarrow \Delta ABC \backsim \Delta A'BC\)

Từ bài tập 2 trang 57 Sách giáo khoa Toán 8 – Cánh diều ta có kết quả: Đường thẳng song song với hai đáy của hình thang thì định ra trên hai cạnh bên các đoạn thẳng tỉ lệ.
Do các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau nên ta có các hình thang ACC’A’, BDD’B’.
Xét hình thang ACC’A’ với BB’ song song với hai đáy AA’ và CC’, ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\,\,\left( 1 \right)\)
Xét hình thang BDD’B’ với CC’ song song với hai đáy BB’ và DD’, ta có:
\(\frac{{BC}}{{CD}} = \frac{{B'C'}}{{C'D'}} \Rightarrow \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CD}}{{C'D'}}\)
Vậy độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A’B’, B’C’, C’D’.



a) Vì MN là đường trung bình của tam giác ABC nên M là trung điểm AB và N là trung điểm AC.
Khi đó \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) suy ra \(MN\parallel BC\) (Định lý Thales đảo trong tam giác ABC).
b) M là trung điểm AB nên \(\frac{{AM}}{{AB}} = \frac{1}{2}\).
Xét tam giác ABC với \(MN\parallel BC\) ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{2}\) (Hệ quả của định lý Thales)