Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c, xét tam giác BEM và tam giác AFM có:
BE=AF(câu b)
BM=AM(do AM là trung tuyến của tam giác cân)
góc EBM =góc MAF(cùng phụ với góc ADM= góc BDE)
suy ra 2 tam giác trên bằng nhau
suy ra góc EMB= góc AMF( 2 góc tương ứng)
mặt khác: góc AMF+góc FMB=90 độ (câu a)
suy ra góc EMB+ góc FMB=90 độ
hay FM vuông góc với ME
hay tam giác EMF vuông tại M
chị làm đó rồi nhé

a./ \(\Delta BEM=\Delta CFM\)vì:
- góc BEM = góc CFM ( = 90o )
- góc EBM = góc FCM (2 góc bằng nhau của tam giác cân ABC tại A)
- => góc EMB = góc FMC ( = 180o - 2 góc bằng nhau)
- MB = MC (vì AM là trung tuyến).
b./ => ME = MF (cạnh tương ứng của 2 tam giác bằng nhau) => M nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (1)
\(\Delta BEM=\Delta CFM\)=> BE = CF => AE = AF ( vì cùng bằng AB - BE = AC - CF)
=> A nằm trên trung trực của EF (vì cách đều 2 đầu của EF) (2)
Từ (1) (2) => AM là trung trực của EF.

a: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)
Do đó: ΔEMB=ΔFMC
Suy ra: BE=CF
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó; BECF là hình bình hành
Suy ra: BF//CE

a/ Xét tam giác BEM và tam giác CMF có:
góc BEM = góc CFM = 900
BM = MC (M là trung điểm của BC)
góc BME = góc CMF (đối đỉnh)
Do đó: tam giác BEM = tam giác CMF (cạnh huyền - góc nhọn)
Vậy: tam giác BEM = tam giác CMF.
b/ Ta có:
BE vuông góc với AM, CF vuông góc với AM => BE// CF
Vậy: BE//CF
c/ Ta có:
tam giác BEM = tam giác CMF (cmt) =>ME = MF
=> M là trung điểm của EF
Vậy: M là trung điểm của EF
(mấy kí hiệu bạn tự viết nha)

A E B C F I M D
a) Xét tam giác BEM và tam giácCFM
có:BM=MC(gt)
góc EBM=gócFCM(tam giác ABC can^)
->T/g BEM=t/g CFM(c.huyền g. nhon)
b)
Xét tam giác vg AEM va t/g vg AFM
có:EM=MF(t/g BEM=t/gAFM)
AM là cạnh chung
->t/g AEM =t/g AFM( c/ huyền -c.góc vg)
->AE=AF(2 cạnh tương ứng)
Xét tam giác AEI và t/g AFI
có:MF=EM(t/g BEM= t/g CFM)
AM là cạnh chung
AF=AE(C/ m trên)
->t/g AEI =t/g AFI(c-c-c)
->EI = IF(2 cạnh tương ứng)
->góc AIE= góc AIF(2 tương ứng)
=>AE là đường trung trực của EF
c(mik ko pt lm)
a và b bạn Hương Sơn
c) Ta có:
\(\Delta ABC\)cân
có AM là đường trung tuyến
=> AM cũng là đường trung trực
=> \(AM\perp BC\)
=> AM = 90 độ
Vì \(\Delta ABC\)cân
=> Góc ABM = góc ACM (1)
mà Góc ABD = góc ACD = 90 độ (2)
Từ (1) và (2) => Góc MBD = góc MCD
Xét \(\Delta DMB\)và \(\Delta DMC\)có :
DM : cạnh chung (1)
Góc MBD = góc MCD ( chứng minh trên ) (2)
BM = MC ( vì AM là đường trung tuyến của tam giác ABC ) (3)
Từ (1) ; (2) và (3) => \(\Delta DMB=\Delta DMC\)(cạnh - góc - cạnh)
=> Góc CMD = góc BMD ( cặp góc tương ứng)
Mà Góc CMD + góc BMD = 180 độ
=> Góc CMD = BMD = 180 : 2 = 90 độ
Vì Góc AMC = 90 độ ( vì AM là đường trung trực)
và góc CMD = 90 độ
=> AMC + CMD = AMD
=> 90 + 90 = AMD
=> AMD = 180 độ
=> Ba điểm A ; M ; D thẳng hàng. ( điều phải chứng minh)
Chúc bạn học tốt !
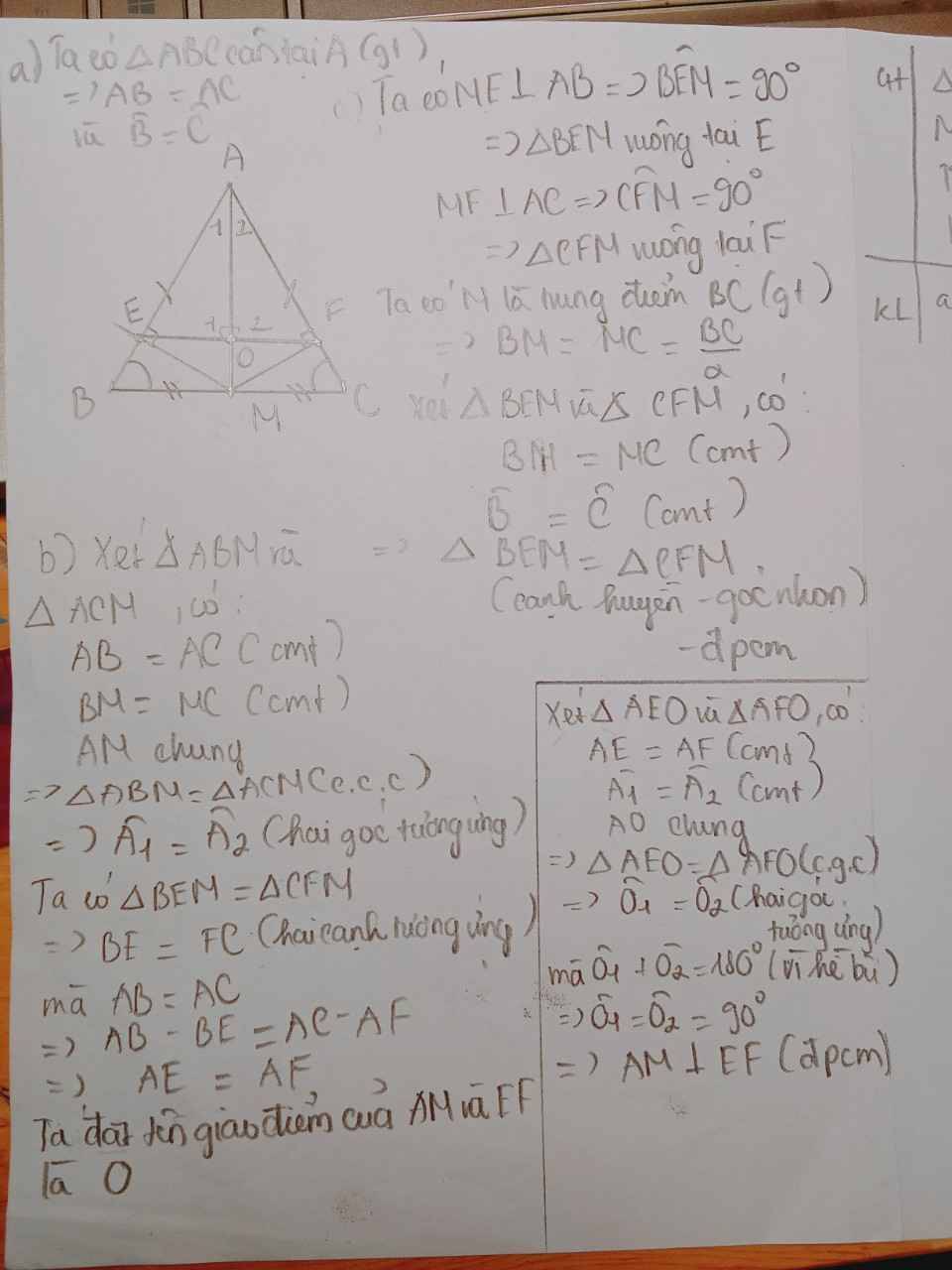
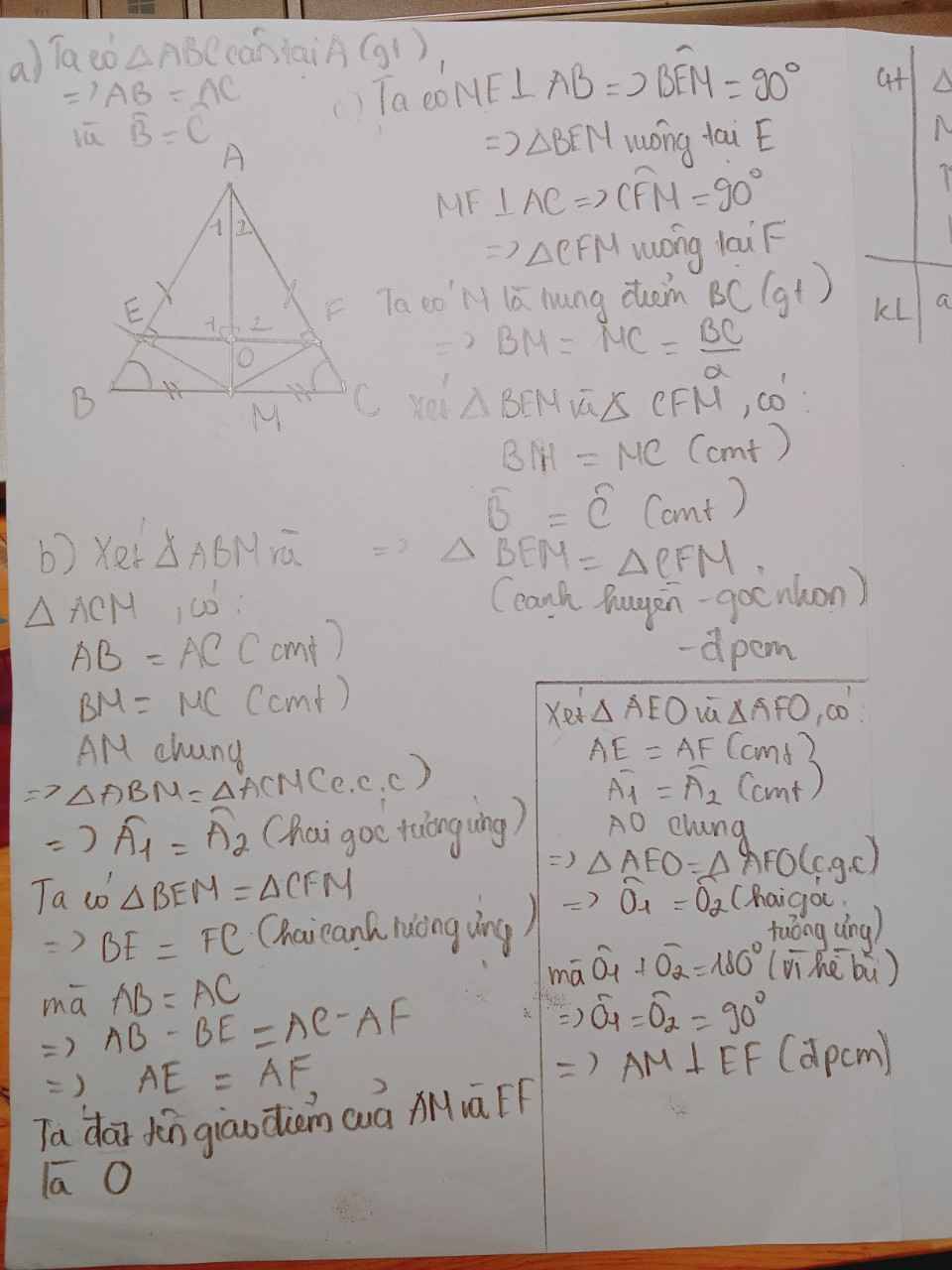
a) Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC(M là trung điểm của BC)
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
Do đó: ΔBEM=ΔCFM(cạnh huyền-góc nhọn)
b) Ta có: ΔBEM=ΔCFM(cmt)
nên BE=CF(hai cạnh tương ứng)
c) Xét ΔBMF và ΔCME có
MB=MC(M là trung điểm của BC)
\(\widehat{BMF}=\widehat{CME}\)(hai góc đối đỉnh)
MF=ME(ΔCFM=ΔBEM)
Do đó: ΔBMF=ΔCME(c-g-c)
⇒\(\widehat{BFM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BFM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên BF//CE(Dấu hiệu nhận biết hai đường thẳng song song)