Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H M N
a) Vì AB = AC =10cm => (đpcm)
b) Xét \(\Delta AHB\)và \(\Delta AHC\)có;
AB = AC(gt)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
AH chung
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\)
\(\Rightarrow HB=HC\)(2 cạnh tương ứng)(1)
\(\Rightarrow\widehat{B}=\widehat{C}\)(2 góc tương ứng)(2)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\Rightarrow\)AH là tia phân giác của \(\widehat{A}\)
c) HM với HN?
Vì \(\Delta HMB;\Delta HNC\)là tam giác vuông nên từ (1);(2) =>\(\Delta HMB=\Delta HNC\)
e)Xét \(\Delta AHC\)vuông:
Áp dụng định lí Py ta go ta có:
\(AC^2=CH^2+AH^2\)
\(12^2=6^2+AH^2\)
\(\Rightarrow AH^2=12^2-6^2=144-36=108\)
\(\Rightarrow AH=\sqrt{108}cm\)

tự kẻ hình nghen :33333
a) Xét tam giác AHB và tam giác AHC có
AH chung
AHC=AHB(=90 độ)
AB=AC(gt)
=> tam giác AHB= tam giac AHC(ch-cgv)
b) từ tam giác AHB= tam giác AHC=> A1=A2( hai góc tương ứng )
Xét tam giác AMH và tam giác ANH có
A1=A2(cmt)
AH chung
AMH=ANH(=90 độ)
=> tam giấcMH=tam giác ANH(ch-gnh)
=> AM=AN( hai cạnh tương ứng)
=> tam giác AMN cân A
c) vì tam giác AMN cân A
=> AMN=ANM=(180-MAN)/2
vì tam giác ABC cân A
=> ABC=ACB=(180-BAC)/2
=> AMN=ABC mà AMN đồng vị với ABC=> MN//BC

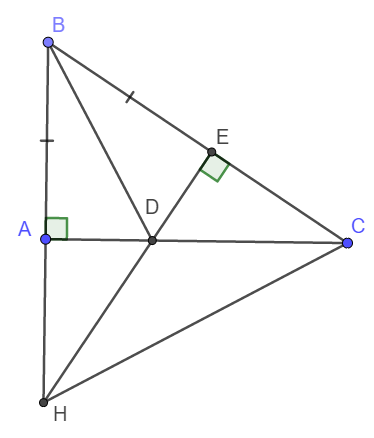
a) Xét tam giác vuông ABD và tam giác vuông EBD có:
Cạnh BD chung
BA = BE (gt)
\(\Rightarrow\Delta ABD=\Delta EBD\) (Cạnh huyền - cạnh góc vuông)
b) Do \(\Delta ABD=\Delta EBD\Rightarrow AD=ED\)
Xét tam giác vuông ADH và tam giác vuông EDC có:
AD = ED
\(\widehat{ADH}=\widehat{EDH}\)
\(\Rightarrow\Delta ADH=\Delta EDH\) (Cạnh góc vuông, góc nhọn kề)
c) Do \(\Delta ADH=\Delta EDH\Rightarrow AH=EH\)
Lại có BA = BE nên BH = BA AH = AE + EC = BC
Xét tam giác HBC có BH = BC nên HBC là tam giác cân.
cho tam giác abc, h là trực tâm, I là GĐ của các đường trung trực (tâm đường tròn ngoại tiếp). Gọi E là điểm đối xứng với A qua I.
CMR : BHCE là hình bình hành
TU GIAI ĐÊ