Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M 4cm H K
a)Ta có: tam giác ABC là tam giác cân
\(=>AB=AC\)
Mà \(AB=4cm\)
=>>AC=4cm
b) Nếu góc B=60 độ =>tgiác ABC là tam giác đèu(t/c)
c) Xét tam giác ABM và tgiác ACM có
AB=AC(cmt)
AM: chung
==>>tgiác ABM=tgiác ACM( ch-cgv)
d) Ta có: tam giác ABM=tgiác ACM(cmt)
=>\(\widehat{AMC}=\widehat{AMB}\)(2 góc tương ứng)
Mà: \(\widehat{AMC+}\widehat{AMC}=180^0\)
\(=>\widehat{AMC=}\widehat{AMB}=\frac{180^0}{2}=90^0\)
=> AMvuông góc vs BC
e) Xét tgiác BMH và tgiác CMK có :
BM=CM( 2 cạnh tương ứng , cmt(a))
\(\widehat{B}=\widehat{C}\)( tgiác ABC là tgiác đều)
==>>>tgiác BMH=tgiác CMK(ch-gn)
=>MH=MK( 2 cạnh tương ứng)

#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`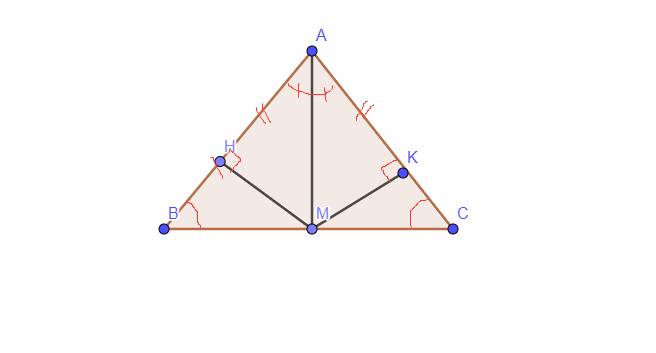

K
Hình hơi xấu hì hì! tự viết GT KL nha!
Cm:
a) \(\Delta ABC\)cân tại A (gt)
=> AB=AC
=>AC=4cm (vì AB=4cm(gt))
Vậy AC=4cm.
b) \(\Delta ABC\)cân tại A (gt)
=>\(\widehat{B}=\widehat{C}\)
\(\Delta ABC\)có:\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(ĐL tổng 3 góc trong 1 tam giác)
\(\Rightarrow60^0+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}=\widehat{C}=60^0\)
=> \(\Delta ABC\)đều.
c) Xét \(\Delta ABM\)và \(\Delta ACM\)có:
AM chung
AB=AC
BM=CM
=>\(\Delta ABM\)=\(\Delta ACM\) (c.c.c)
(đpcm)
d) Vì \(\Delta ABM\)=\(\Delta ACM\)(cmt)
=>\(\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(2 góc kề bù)
=>\(\widehat{AMB}=\widehat{AMC}=90^0\)
=> \(AM⊥BC\)(Đpcm)
e)Xét \(\Delta BHM\)và \(\Delta CKM\)có:
\(\widehat{BHM}=\widehat{CKM}=90^0\)
BM=CM
\(\widehat{B}=\widehat{C}\)
=>\(\Delta BHM\)=\(\Delta CKM\)(cạnh huyền-góc nhọn)
=>MH=MK(2 cạnh t/ứ)
(đpcm)

AB = AC => ABC cân tại A
M trung điểm BC => AMB = AMC
=> MH chiều cao của AMB từ M
=> MK chiều cao của AMC từ M
=> MH = MK

a:
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
b: Xét ΔABC có
AM là đường trung tuyến
AM là đường phân giác
Do đó: ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)

a, xét tam giác MBH và tam giác MCK ta có:
góc MHB= góc MKC=90 độ
BM=MC(gt)
góc B =góc C(gt)
vậy tam giác BMH = tam giác CMK(ch-gn)
b, xét tam giác AMH và tam giác AMK có:
AM chung
MH=MK( do tam giác BMH= tam giác CMK)
góc AHM= góc AKM=90 độ
suy ra tam giác AMH= tam giác AMK( ch-cgv)

A)do AM là tia phân giác của ^A
\(\Rightarrow\)MH=MK(tính chất tia phân giác)
b)theo bài ra M là trung điểm của BC nên AM vừa là phân giác vừa là trung tuyến của tam giác ABC
Suy ra \(\Delta ABC\)cân tại A\(\Leftrightarrow\)góc B =góc C

a) tam giác AMH và tam giác AMK có
góc AHM = góc AKM ( = 90 độ)
chung AM
góc HAM = góc MAK ( AM là phân giác góc A)
=> tam giác AMH = tam giác AMK ( ch - gn)
=> MH = MK (cạnh tương ứng)
b)
tam giác ABC có AM vừa là trung tuyến đồng thời là phân giác góc A
=> tam giác ABC cân tại A (dhnb) => góc B = góc C (tc tam giác cân)
a) tam giác AMH và tam giác AMK có
góc AHM = góc AKM ( = 90 độ)
chung AM
góc HAM = góc MAK ( AM là phân giác góc A)
=> tam giác AMH = tam giác AMK ( ch - gn)
=> MH = MK (cạnh tương ứng)
b)
tam giác ABC có AM vừa là trung tuyến đồng thời là phân giác góc A
=> tam giác ABC cân tại A (dhnb) => góc B = góc C (tc tam giác cân)