Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??

Do G là trọng tâm ABC \(\Rightarrow\overrightarrow{BG}=\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
I đối xứng B qua G \(\Rightarrow\) \(\overrightarrow{BI}=2\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}=-\dfrac{4}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{CI}=\overrightarrow{CB}+\overrightarrow{BI}=\overrightarrow{CA}+\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{CI}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)

Bài 2:
vecto AM=vecto AB+vecto BM
=vecto AB+2/3vecto BC
=vecto AB+2/3*(vecto BA+vecto AC)
=1/3*vecto AB+2/3*vecto AC

Do G là trọng tâm tam giác
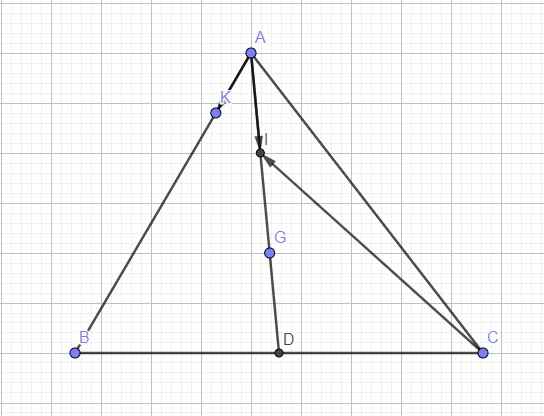
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)

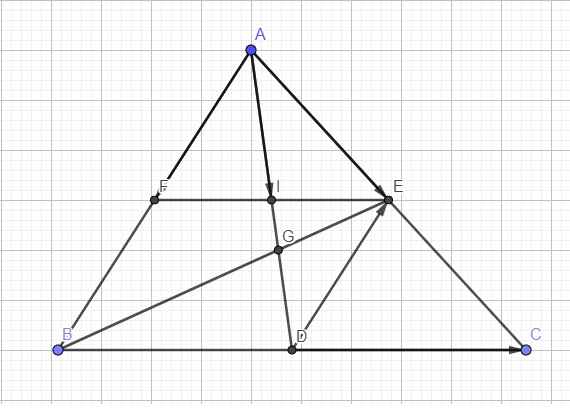
F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)

Khai thác giả thiết:
+ IA =2IB <=> IA = 2( AB -AI) <=> IA = -2AB <=> AI = 2AB
+ 3JA + 2JC =0 <=> 3JA + 2(JA+ AC) =0 <=> JA = ( -2/5)AC <=> AJ = (2/5) AC
Chỉ ra được vị trí các điểm I, J:
+ I đối xứng với A qua B ( tức B là trung điểm AI)
+ J nằm trên đoạn AC sao cho AJ = 2/5 AC
* Ta có:
+ GI = GA + AI = GA + 2AB
+ GJ = GA + AJ = GA + (2/5) AC
Suy ra:
GI - 5 GJ = -4 GA + 2(AB - AC) = -4GA + 2CB = -4GA + 2(GB -GC)
= -2GA +4GB ( chỗ này có áp dụng tính chất trọng tâm: GA +GB + GC =0)
Do B là trung điểm của AI => 2GB = GA +GI
Suy ra:
GI - 5 GJ = -2GA + 2GA + 2 GI
=> GI = - 5 GJ
Đẳng thức này suy ra I, J, G thẳng hàng => IJ đi qua G (đpcm)
I, J, G thẳng hàng
Do I đối xứng A qua B \(\Rightarrow\overrightarrow{AI}=2\overrightarrow{AB}\)
Do G là trọng tâm tam giác \(\Rightarrow\overrightarrow{AG}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{GA}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)
a.
\(\overrightarrow{GI}=\overrightarrow{GA}+\overrightarrow{AI}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}+2\overrightarrow{AB}=\dfrac{5}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)
b.
\(\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{JC}=\dfrac{2}{3}\overrightarrow{JA}+\dfrac{2}{3}\overrightarrow{AC}\Rightarrow\dfrac{5}{3}\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AJ}=\dfrac{2}{5}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}+\overrightarrow{GJ}=\dfrac{2}{5}\overrightarrow{AC}\Rightarrow\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}+\overrightarrow{GJ}=\dfrac{2}{5}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{GJ}=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{15}\overrightarrow{AC}=-\dfrac{1}{5}\left(\dfrac{5}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\right)=-\dfrac{1}{5}\overrightarrow{GI}\)
\(\Rightarrow\) G,I,J thẳng hàng
vecto DM=veto DB+vecto BM
=-vecto BD+1/2vecto BC
=-2vecto BG+1/2vecto BC
GọiK là giao của BG với AC
=>Klà trung điểm của AC
=>\(\overrightarrow{BG}=\dfrac{2}{3}\cdot\overrightarrow{BK}\)
=>\(\overrightarrow{DM}=-2\cdot\dfrac{2}{3}\cdot\overrightarrow{BK}+\dfrac{1}{2}\overrightarrow{BC}\)
\(=\dfrac{-4}{3}\cdot\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)+\dfrac{1}{2}\overrightarrow{BC}\)
\(=\dfrac{-2}{3}\overrightarrow{BA}-\dfrac{2}{3}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{BC}\)
\(=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{BC}\)
\(=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{6}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{5}{6}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AC}\)