Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Ta có:
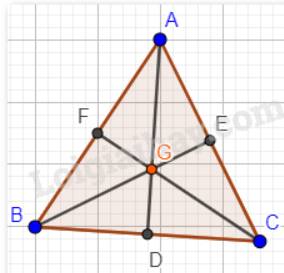
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
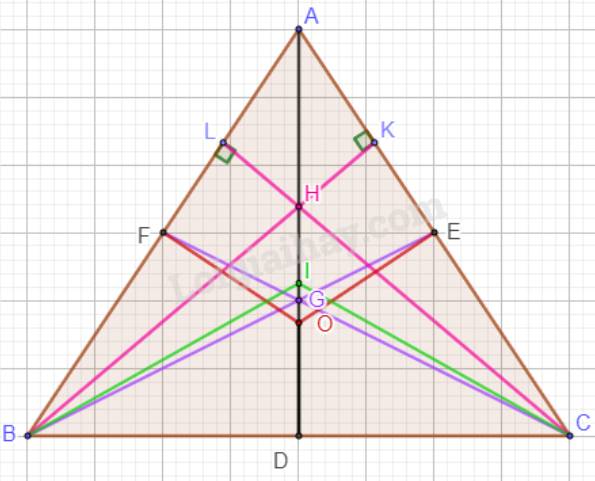
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.

a)
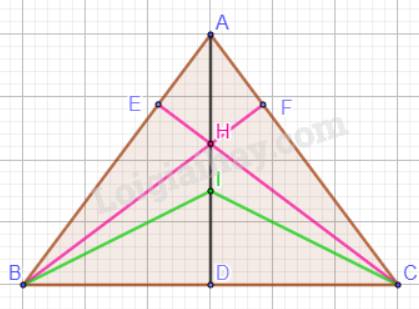
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC (D là trung điểm của BC).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A.
Suy ra: AD là đường trung trực của tam giác ABC.
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC.
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng).
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.

Nguyễn Thị Hội là con nào????????????????????????????????????????????????????????????????????????????????????????
) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD \Rightarrow OM là đường trung bình của Δ BCD
\Rightarrow OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) \Rightarrow DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) \Rightarrow AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
\RightarrowΔABH=ΔBAD( g-c-g )
\Rightarrow AH = BD mà OM=12DB \Rightarrow OM=12AH
\Rightarrow AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A \Rightarrow PQ là đường trung bình của \large\Delta AG'H
\RightarrowPQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH\Rightarrow PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH\Rightarrow PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
\Rightarrow ΔPQG′=ΔOMG′( g-c-g )
\Rightarrow G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) \Rightarrow G′M=12G′Amà G'M + G'A = AM
\Rightarrow G′A=23AM mà AM là trung tuyến của ΔABC
\Rightarrow G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC \RightarrowG′≡ G
mà G′∈OH \RightarrowG∈OH \Rightarrow O, H, G thẳng hàng ( đpcm )

Trọng tâm : điểm giao nhau của 3 đường trung tuyến trong Tam giác
Trực tâm : giao giữa ba đường cao
Đường trung trực : là đường vuông góc với 1 đoạn thẳng tại trung điểm của đoạn thẳng đó.
chắc giờ trả lời là trễ lắm rồi, 2021 cơ mà. Nhưng lỡ thì kệ đi.

) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD OM là đường trung bình của Δ BCD
OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
ΔABH=ΔBAD( g-c-g )
AH = BD mà OM=12DB OM=12AH
AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A PQ là đường trung bình của \large\Delta AG'H
PQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
ΔPQG′=ΔOMG′( g-c-g )
G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) G′M=12G′Amà G'M + G'A = AM
G′A=23AM mà AM là trung tuyến của ΔABC
G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC G′≡ G
mà G′∈OH G∈OH O, H, G thẳng hàng ( đpcm )
Hên xui nghe bạn ^ ^

a) Trên tia đối của tia OC lấy điểm N sao cho ON = OC,ta có : \(OM//BN\)và \(OM=\frac{1}{2}BN\)
Vì OM \(\perp\)BC,AH \(\perp\)BC,do đó OM //AH => NB // AH
Cmtt NA/BH
Xét \(\Delta\)ANB và \(\Delta\)BHA có :
AN = AH(gt)
\(\widehat{A_1}=\widehat{A_2}\)(gt)
\(\widehat{B_1}=\widehat{B_2}\)(gt)
=> \(\Delta ANB=\Delta BHA\left(g.c.g\right)\)
=> NB = AH(hai cạnh tương ứng)
Mà \(OM=\frac{1}{2}NB\)
=> AH = 2OM
b) Gọi I là trung điểm của AG,K là trung điểm của HG thì IK//AH => IK//OM,do đó \(\widehat{KIG}=\widehat{OMG}\)(so le trong)
Xét \(\Delta KGI\)và \(\Delta OMG\)có :
GI = GM(gt)
\(\widehat{G_1}=\widehat{G_2}\)(đối đỉnh)
\(\widehat{I}=\widehat{M}\)
=> \(\Delta KGI=\Delta OGM\left(g.c.g\right)\)
=> KG = GO
Từ đó ta có : HG = GO.

bn vẽ hình giùm mk đi, hoặc giải thích thế nào là trực tâm, trọng tâm z?