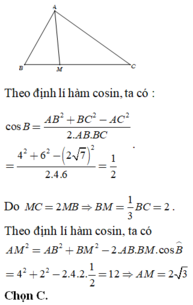Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\left|\overrightarrow{AC}+\overrightarrow{AC}\right|=2\cdot AC=2a\)
b: Gọi M là trung điểm của BC
=>BM=CM=a/2
\(AM=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=a\sqrt{3}\)

a/ \(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AE}\\\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AE}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AM}+\overrightarrow{AN}\)
b/ \(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IA}+2\overrightarrow{IE}=2\left(\overrightarrow{IA}+\overrightarrow{IE}\right)=2\overrightarrow{0}=\overrightarrow{0}\)
c/ \(2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=2\left(\overrightarrow{OI}+\overrightarrow{IA}\right)+\overrightarrow{OI}+\overrightarrow{IB}+\overrightarrow{OI}+\overrightarrow{IC}\)
\(=\left(2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+4\overrightarrow{OI}=\overrightarrow{0}+4\overrightarrow{OI}=4\overrightarrow{OI}\)

Lời giải:
Lấy điểm $N$ trên $AB$ sao cho $MN\parallel AC$
Ta có:
\(\overrightarrow{AM}=\overrightarrow{AN}+\overrightarrow{NM}=\frac{AN}{AB}.\overrightarrow{AB}+\frac{NM}{AC}.\overrightarrow{AC}\)
Mà:
\(\frac{AN}{AB}=\frac{MC}{BC}; \frac{NM}{AC}=\frac{MB}{BC}\) theo định lý Ta-let với $MN\parallel AC$
\(\Rightarrow \overrightarrow{AM}=\frac{MC}{BC}\overrightarrow{AB}+\frac{MB}{BC}\overrightarrow{AC}\)
Ta có đpcm.

Chọn C.
Theo định lí hàm cosin, ta có : ![]()
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: ![]() .
.