Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Nối DD và FF
Xét ΔBDFΔBDF và ΔDEFΔDEF , ta có :
DF=DFDF=DF ( cạnh chung )
ˆBDF=ˆDEFBDF^=DEF^ ( vì AB//EFAB//EF )
ˆDFB=ˆFDEDFB^=FDE^ ( vì DE//BCDE//BC )
⇒ΔBDF=ΔFDE(g.c.g)⇒ΔBDF=ΔFDE(g.c.g)
⇒DB=EF⇒DB=EF ( hai cạnh tương ứng )
Mà AD=DB⇒AD=EFAD=DB⇒AD=EF
b. Xét ΔADEΔADE và ΔEFCΔEFC , ta có :
ˆA=ˆFECA^=FEC^ ( vì AB//EFAB//EF )
AD=EFAD=EF ( theo câu a )
ˆADE=ˆEFC(=ˆB)ADE^=EFC^(=B^)
⇒ΔADE=ΔEFC(g.c.g)

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC

NGU NHƯ BÒÔFÔFÒÔFÔFÔFFÒÔFFÔFOFOFÔFỒ
RỨA MÀ KHÔNG LÀM ĐƯỢC NGU VL NGU VCL NGU VÃI LINH HỒN NGU VÃI L*N CHIM ÉN
xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g)
--> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB)
nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)
c) tam giac ADE= tam giac EFC (cmt)--> AE=EC

Cứng đờ tay luôn rồi, khổ quá:((
a) Xét \(\Delta DBF\) và \(\Delta FED:\)
DF:cạnh chung
\(\widehat{BDF}=\widehat{EFD}\)(AB//EF)
\(\widehat{BFD}=\widehat{EDF}\)(DE//BC)
=> \(\Delta BDF=\Delta EFD\left(g-c-g\right)\)
b) (Ở lớp 8 thì sé có cái đường trung bình ý bạn, nó sẽ có tính chất luôn, nhưng lớp 7 chưa học đành làm theo lớp 7 vậy)
Ta có: \(\widehat{DAE}+\widehat{AED}+\widehat{EDA}=180^o\) (Tổng 3 góc trong 1 tam giác)
Lại có: \(\widehat{AED}+\widehat{DEF}+\widehat{FEC}=180^o\)
Mà \(\widehat{DEF}=\widehat{EDA}\)(AB//EF)
=>\(\widehat{DAE}=\widehat{FEC}\)
Xét \(\Delta DAE\) và \(\Delta FEC:\)
DA=FE(=BD)
\(\widehat{DAE}=\widehat{EFC}\left(=\widehat{DBF}\right)\)
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=>\(\Delta DAE=\Delta FEC\left(g-c-g\right)\)
=> DE=FC(2 cạnh t/ứ)
=> Đpcm

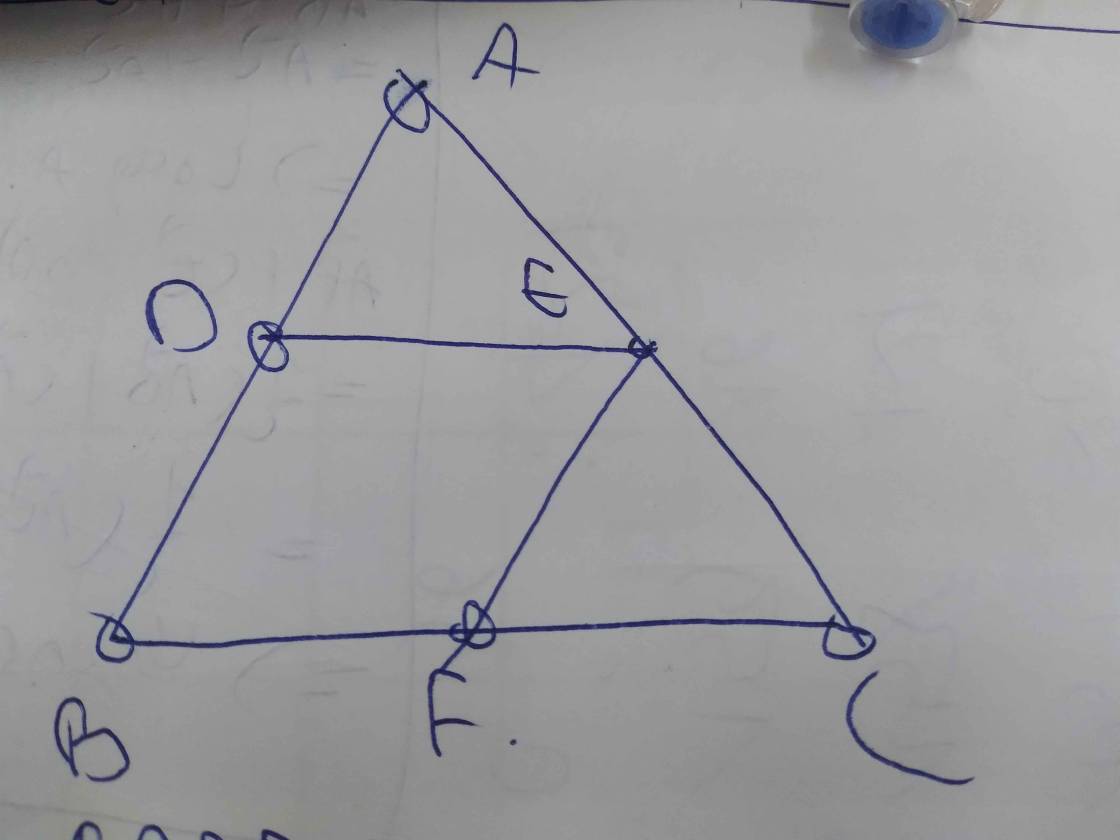
A B C D E F
Xét tam giác BDF và tam giác DEF ta có:
DF=DF (cạnh chung)
\(\widehat{BDF}=\widehat{DFE}\)(2 góc so le trong ;BA//EF)
\(\widehat{DFB}=\widehat{FDE}\)(2 góc so le trong ; DE//BC)
=> \(\Delta BDF=\Delta DEF\left(g.c.g\right)\)
=> \(BD=EF\)(2 cạnh tương ứng)
Mà AD=BD(D là trung điểm của AB gt)
Nên AD=EF
b) \(\widehat{ADE}=\widehat{BAC}\)(2 góc đồng vi,DE//BC)
\(\widehat{CEF}=\widehat{BAC}\)(2 góc đồng vi,EF//AB)
\(\Rightarrow\widehat{ADE}=\widehat{CFE}\)( phần này mình ko chắc)
Xét \(\Delta ADE=\Delta EFC\)
\(\widehat{ADE}=\widehat{CFE}\Rightarrow AD=EF\)(chứng minh theo câu a)
\(\widehat{DAE}=\widehat{FEC}\)(2 góc đồng vi ;DE//BC)
\(\Leftrightarrow\Delta ADE=\Delta EFC\left(g.c.g\right)\)
Từ đó,ta có \(\Delta ADE=\Delta EFC\)
\(\Rightarrow AE=EC\)(2 cạnh tương ứng)
Vì DE//BC
\(\widehat{F_2}\)=\(\widehat{D_1}\)(SLT)
Vì EF//AB
\(\Rightarrow\widehat{F_1}\)=\(\widehat{D_2}\)(SLT)
Xét \(\Delta BDFvà\Delta EDF\)
\(\widehat{F_2}=\widehat{_{ }D_1}\)(c.m.tr) \(\widehat{D_2}=\widehat{F_1}\left(c.m.tr\right)\)\(DF\)là cạnh chung
\(\Rightarrow\Delta BDF=\Delta EDF\left(g.c.g\right)\)
\(BD=EF\)(2 cạnh t/ứng) và\(\widehat{D}=\widehat{E}\)(2 góc t/ứng)
\(\Rightarrow BD=AD=EF\)
Xét \(\Delta ADEvà\Delta EFC\)
AD=EF D\(\widehat{D_3}=\widehat{F_3}\left(c.m.tr\right)\) \(\widehat{A}=\widehat{E}\)
\(\Rightarrow\Delta ADE=\Delta EFC\left(g.c.g\right)\)
\(\Rightarrow\)AE=EC(2 canh..)

a: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Suy ra: EF=BD
mà BD=AD
nên EF=AD
b: Xét ΔADF và ΔFEA có
AD=FE
AF chung
DF=EA
Do đó: ΔADF=ΔFEA