K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

13 tháng 1 2021
a) Xét ΔACD và ΔAEB có
AD=AB(ΔABD đều)
\(\widehat{CAD}=\widehat{BAE}\left(=60^0+\widehat{BAC}\right)\)
AC=AE(ΔACE đều)
Do đó: ΔACD=ΔAEB(c-g-c)
⇒CD=BE(hai cạnh tương ứng)
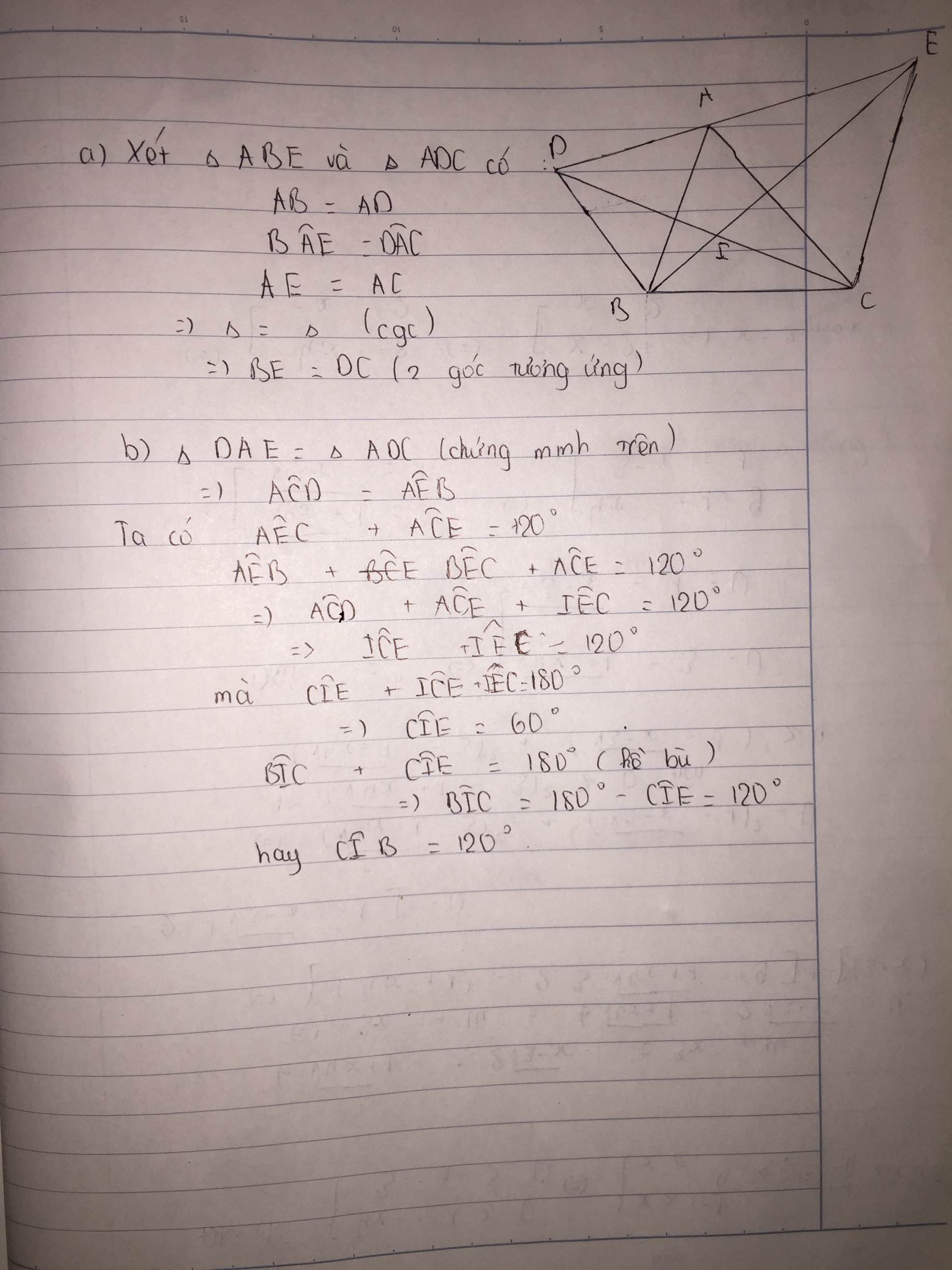
Gọi I là giao điểm của AB và DC
△ADC△ADC và △ABE△ABE có:
AD=ABAD=AB
ˆDAC=600+ˆBAC=ˆBAEDAC^=600+BAC^=BAE^
AC=AEAC=AE
Nên △ADC=△ABE△ADC=△ABE (c.g.c) do đó ˆIDA=ˆABMIDA^=ABM^
Xét △ADI△ADI và △MIB△MIB có
ˆIDA=ˆABMIDA^=ABM^
ˆDIA=ˆMIBDIA^=MIB^ (đối đỉnh)
Nên ˆBMI=ˆIAD=600BMI^=IAD^=600
Vậy ˆBMC=1800−ˆBMI=1200BMC^=1800−BMI^=1200
Gọi N thuộc tia đối của ME sao cho MN=MDMN=MD thì △MND△MND đều do cóMN=MDMN=MD và ˆBMI=600BMI^=600
Xét △ADM△ADM và △DBN△DBN có:
AD=BDAD=BD
ˆADM=ˆBDN=600−ˆBDMADM^=BDN^=600−BDM^
DM=DNDM=DN
Nên △ADM△ADM và △BDN△BDN (c.g.c) do đó ˆAMD=ˆBND=600AMD^=BND^=600
Vậy ˆAMB=ˆAMD+ˆDMB=1200AMB^=AMD^+DMB^=1200
coppy mạng lỗi hết bài rồi kìa Nam :))