Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEH=góc ADH=góc DAE=90 độ
=>AEHD là hình chữ nhật
b: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồng dạng với ΔAHB
c: ΔAHC vuông tại H có HE vuông góc AC
nên HE^2=AE*EC

a: góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạngvói ΔAHD
c: ΔHAC vuông tại H có HE là đường cao
nên HE^2=AE*EC

a)xét tam giác abh và tam giác ahd có :
góc A chung
góc AHB = góc ADH(=90 độ )
=>tam giác abh đồng dạng với tam giác ahd (g.g)
b)xét tam giác hec và tam giác aeh có ;
góc AEH =góc CEH(=90độ )
góc HAE=góc EHC (vì cùng phụ với góc AHE)
=>tam giác hec đồng dạng với tam giác AEH(g.g)
=>HE/EC=AE/EH
=>HE^2=AE.EC(dpcm)

Bài 1 :
a, Xét tam giác BDA và tam giác KDC có:
Góc BDA= Góc KDC(đối đỉnh)
Góc B= Góc K(90 độ)
=>Tam giác BDA đồng dạng với tam giác KDC(g.g)
b,
Tam giác BDA đồng dạng với tam giác KDC ( cmt) => \(\frac{DB}{DA}=\frac{DK}{DC}\)
Xét tam giác DBK và tam giác DAC có:
Góc BDK= Góc DAC(đối đỉnh)
\(\frac{DB}{DA}=\frac{DK}{DC}\)
=>Tam giác DBK đồng dạng với tam giác DAC(c.g.c)
Bài 2 :
a) Xét tam giác ABH và tam giác AHD có:
\(\widehat{A}chung\)
\(\widehat{AHB}=\widehat{ADH}=90^o\)
⇒ tam giác ABH đồng dạng với tam giác AHD (g-g)
b)T/tự: tam giác AHC đồng dạng với tam giác AEH (g-g)
⇒ \(\widehat{ACH}=\widehat{AHE}\) ( 2 góc tương ứng)
Tam giác AEH đồng dạng với tam giác HEC
\(\widehat{ACH}=\widehat{AHE}\) (CM trên)
và \(\widehat{AEH}=\widehat{HEC}\) (= 900)
⇒\(\frac{AE}{HE}=\frac{EH}{EC}\)⇒\(AE\cdot EC=EH\cdot EH=EH^2\)
c) tam giác ADC đồng dạng với tam giác ABE (g-g) vì:
\(\widehat{A}\) chung
\(\widehat{ADC}=\widehat{AEB}=90^O\)
⇒ \(\widehat{ACD}=\widehat{ABE}\) ( 2 góc tương ứng)
Xét tam giác DBM và tam giác ECM có:
\(\widehat{ACD}=\widehat{ABE}\) (CM trên)
\(\widehat{DMB}=\widehat{EMC}\) (đối đỉnh)
⇒ tam giác DBM đồng dạng với tam giác ECM (g-g)
Bài 3 :

Bạn tự vẽ hình rồi đối chiếu kq nhé, có thể có sai sót đấy, ko chắc đúng hết đâu
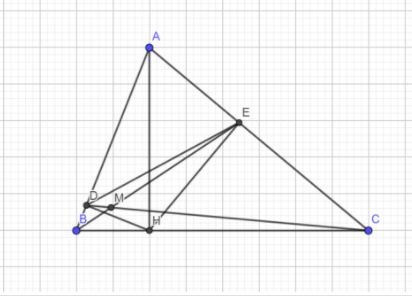


A B C D H E M a, Vì AH là đường cao của ΔABC
⇒ AH ⊥ BC
⇒ \(\widehat{AHB}=\widehat{AHC}=90^0\)
Vì HD ⊥ AB ⇒ \(\widehat{ADH}=90^0\)
ΔABH ~ ΔAHD (g.g)
b, C/m ΔAEH ~ HEC => Đpcm
c,
+) C/m: ΔACH ~ ΔAHE (g.g)
⇒ AH2 = AC.AE (1)
+) Vì ΔABH ~ ΔAHD (câu a)
⇒ AH2 = AB.AD (2)
Từ (1), (2) ⇒ AB.AD = AC.AE
⇒ \(\frac{AB}{AC}=\frac{AE}{AD}\)
Mà BAC chung
⇒ ΔAEB ~ ΔADC (c.g.c)
⇒ DBM^ = ECM^
mà 2 góc M đối đỉnh
⇒ Đpcm