Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C I K G x x x x E D
P/s : Hình vẽ k đc chính xác ! Thông cảm ạ !
a) Ta có : AE = EB
AD = DC
\(\Rightarrow\)ED là đường trung bình của △ABC
\(\Rightarrow\)ED song song và bằng \(\frac{1}{2}\)BC (1)
Lại có : IG = IB
KG = KC
\(\Rightarrow\)IK là đường trung bình của △GBC
\(\Rightarrow\)IK song song và bằng \(\frac{1}{2}\)BC (2)
Từ (1) và (2) suy ra : ED song song và bằng IK
\(\Rightarrow\)Tứ giác DEIK là hình bình hành
Mà EK ⊥ DI
\(\Rightarrow\) Tứ giác DEIK là hình thoi
Có : G là trọng tâm của △ABC
\(\Rightarrow\)GD = \(\frac{1}{3}\)BD
GE = \(\frac{1}{3}\)EC
Vì △ABC cân nên BD = EC
\(\Rightarrow\)\(\frac{1}{3}\)BD = \(\frac{1}{3}\)EC
\(\Rightarrow\)GD = GE
\(\Rightarrow\)2GD = 2GE
\(\Rightarrow\)DI = EK
\(\Rightarrow\)Tứ giác DEIK là hình vuông
b) Ta có :
GE = \(\frac{1}{3}\)CE (Vì G là trọng tâm của △ABC)
\(\Rightarrow\)GE = 4 cm
Vì DEIK là hình vuông
\(\Rightarrow\)△GED vuông cân tại G
Áp dụng định lí Pythagoras vào △GED vuông cân tại G, ta có :
ED2 = GE2 + GD2
\(\Rightarrow\)ED2 = 2GE2
\(\Rightarrow\)ED2 = 2.42
\(\Rightarrow\) ED2 = 32
\(\Rightarrow\)ED = \(\sqrt{32}\)cm
Vậy \(S_{DEIK}=\left(\sqrt{32}\right)^2=32\left(cm^2\right)\)

tam giác ACD có AO=OD(O là giao điểm hai đường chéo)
AM=MD(M là trung điểm AD) suy ra MO là đường trung bình tam giác ACD
=> MO=\(\dfrac{DC}{2}\)=\(\dfrac{16}{2}\)=8 cm
tam giác ACD vuông tại D suy ra AC2= AD2+DC2
AC2= 122+162= 144+256=400
=> AC=\(\sqrt{400}\)=20 cm
tam giác ACD vuông tại D có DO là đường trung tuyến(OB=OD)
suy ra DO= \(\dfrac{AC}{2}\)=\(\dfrac{20}{2}\)=10 cm
tui làm bài 1 thui còn bài còn lại làm biếng

a) Xét tam giác GBC có:
I là trung điểm GB, K là trung điểm GC => IK là đường trung bình tam giác GBC(đpcm)
b) Xét tam giác ABC có:
BD là trung tuyến => D là trung điểm AC
CE là trung tuyến =>E là trung điểm AB
==>> ED là đường trung bình tam giác ABC => ED= 1/2 BC (1) và ED//BC(2)
Ta có: IK là đường trung bình tam giác GBC => IK= 1/2 BC (3) và IK//BC (4)
Từ (1) và (3) => ED=IK (đpcm)
Từ (2) và (4) => ED//IK (đpcm)
K cho mk nha!!!!!

Mình không biết vẽ hình trên đây nên bạn thông cảm nhé
a,Xét tam giác GBC có: GI=BI(I là trung điểm của GB)
GK=CK(K là trung điểm của GC)
=>IK là đường trung bình của tam giác GBC
b, Vì IK là đường trung bình của tam giác GBC
=> \(\hept{\begin{cases}IK=\frac{1}{2}BC\\IKsongsongBC\end{cases}}\)(1)
Vì BD là đường trung tuyến kẻ từ B của tam giác ABC =>AD=CD
Vì CE là đường trung tuyến kẻ từ C của tam giác ABC =>AE=BE
Xét tam giác ABC có: AD=CD
AE=BE
=>DE là đường trung bình của tam giác ABC
=>\(\hept{\begin{cases}DE=\frac{1}{2}BC\\DEsongsongBC\end{cases}}\)(2)
Từ (1) và (2)=>\(\hept{\begin{cases}IK=ED\\IKsongsongED\end{cases}}\)

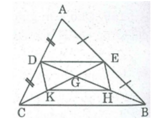
Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.

A B C D E G F I K
a. Xét \(\Delta ABC\)
Ta có \(\hept{\begin{cases}AE=EB\\AD=DC\end{cases}\Rightarrow DE}\)là đường trung bình của tam giác ABC
\(\Rightarrow\)DE song song BC và \(DE=\frac{1}{2}BC\left(1\right)\)
Xét \(\Delta BGC\)có \(\hept{\begin{cases}BI=IG\\CK=KG\end{cases}\Rightarrow IK}\)là đường trung bình của tam giác BGC
\(\Rightarrow\)IK song song BC và \(IK=\frac{1}{2}BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow DE\)song song \(IK\)và \(DE=IK\)
b. Theo tính chất của trọng tâm ta có
\(GF=\frac{1}{3}AF\);\(AG=\frac{2}{3}AF\left(3\right)\)
Xét \(\Delta ABG\)có IE là đường trung bình suy ra \(IE=\frac{1}{2}AG\left(4\right)\)
Từ (3) và (4) \(\Rightarrow IE=\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AF=\frac{1}{3}AF=GF\)
Vậy \(IE=GF\)