Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)

Câu 4:
a: Xét ΔMIN và ΔMIP có
MI chung
IN=IP
MN=MP
Do đó: ΔMIN=ΔMIP

\(a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}BM=MC\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BCD}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}CD\\ c,\left\{{}\begin{matrix}BM=MC\\\widehat{AMC}=\widehat{BMD}\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow\widehat{ACB}=\widehat{CBD}\\ \text{Mà 2 góc này ở vị trí slt nên }AC\text{//}BD\)

Lời giải:
a.
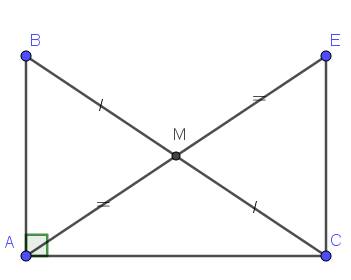
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)

a) Xét tam giác AMB và tam giác AMC ta có:
AM chung
AB=AC (gt)
MB=MC (vì M là trung điểm của BC)
Suy ra tam giác AMB=tam giác AMC (c-c-c) (đpcm)
b) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc BAM=góc CAM (2 góc tương ứng)
Suy ra AM là tia phân giác của góc BAC (đpcm)
c) Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc AMB=góc AMC(2 góc tương ứng)
Mà góc AMB+góc AMC=180 độ (2 góc kề bù)
Suy ra góc AMB=góc AMC=180 độ/2=90 độ
Suy ra AM vuông góc với BC tại M (đpcm)
Vì tam giác AMB=tam giác AMC (cmt)
Suy ra góc ACM=góc ABM (2 góc tương ứng) (đpcm)