Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tg ABD và AED có: AE = AB (gt)
góc BAD = góc EAD
AD chung
DO đó tg ADB = tg AED (c.g.c)
=> BD = DE
=> tam giác BDE cân tại D (đcpm)

E D A C B F I
a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )

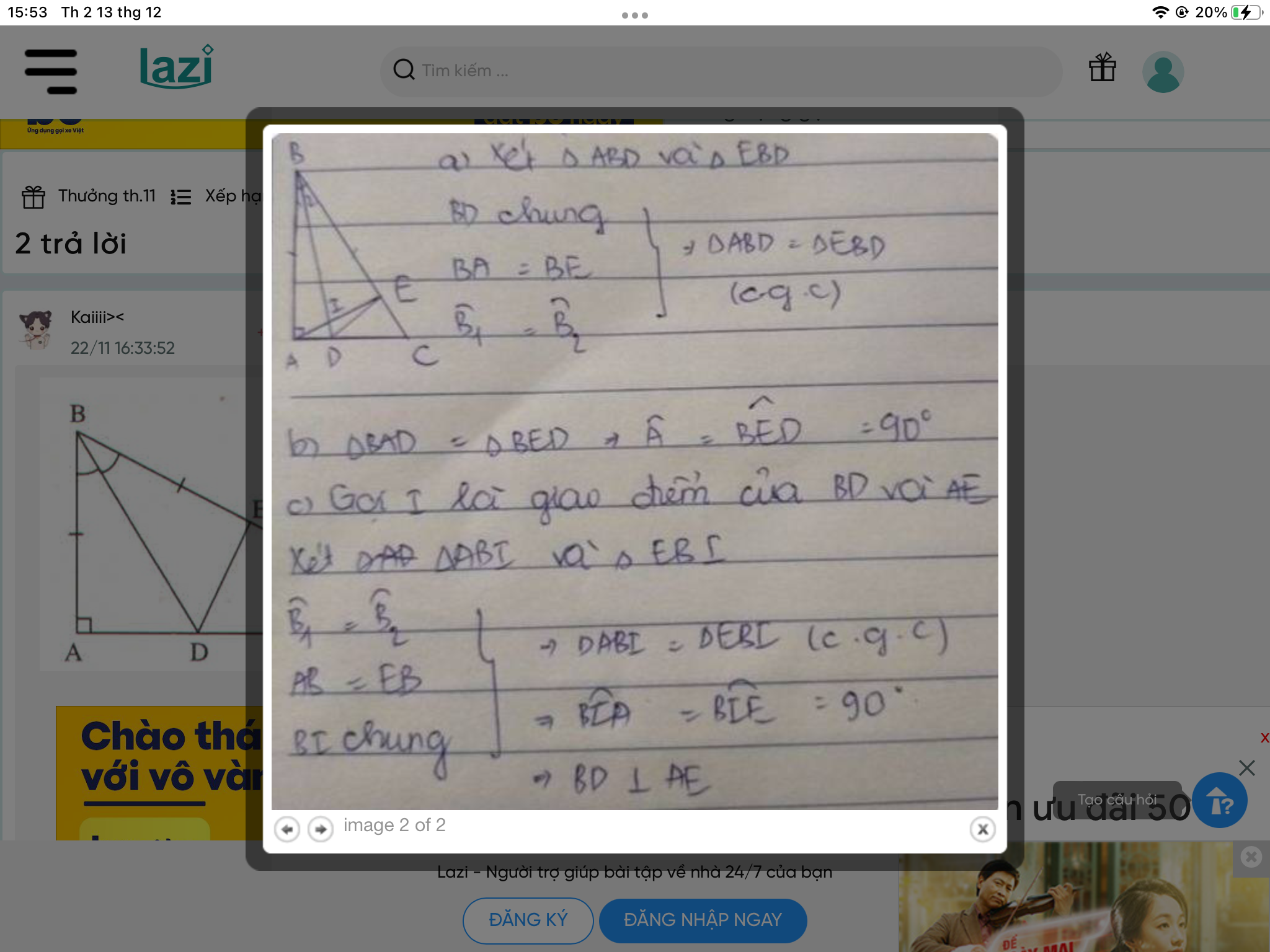
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)
Xét ΔBED có BD=ED(cmt)
nên ΔBED cân tại D(Định nghĩa tam giác cân)
b) Ta có: AB=AE(gt)
nên A nằm trên đường trung trực của BE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DB=DE(cmt)
nên D nằm trên đường trung trực của BE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của BE
hay AD⊥BE tại trung điểm của BE
mà AD cắt BE tại I(gt)
nên AD⊥BE tại I
⇔\(\widehat{AIB}=90^0\)
Vậy: \(\widehat{AIB}=90^0\)
c) Ta có: ΔBDA=ΔEDA(cmt)
nên \(\widehat{BDA}=\widehat{EDA}\)(hai góc tương ứng)
mà tia DA nằm giữa hai tia DE,DB
nên DA là tia phân giác của \(\widehat{BDE}\)(đpcm)
a) Ta chứng minh được ΔABD = ΔAED (c-g-c)
=> BD = DE=> tam giác BDE cân tại D
b) Do ΔABD = ΔAED nên góc BDI = góc EDI
=> ΔBDI = ΔEDI (c-g-c)
=> góc BID = góc EID = 90 độ
=> góc AID = 90 độ
c) Ta có góc BDI = góc EDI
=> DA là phân giác của góc BDE
b, BAE cân tại A có AI là đường phân giác => AI là đường cao => AIB = 90 độ
c, phân giác