Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, góc A + góc B = 120
góc A - góc B = 30
=> góc A = (120 + 30) : 2 = 75
=> GÓC B = 75 - 30 = 45
tam giác ABC => góc A + góc B + góc C = 180
=> góc C = 180 - 120 = 60
=> BC > AB > AC (đl)
b,

Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD

Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.


Trên cạnh AC lấy điểm E sao cho AE = AB.
Ta có: AB < AC nên AE < AC
Suy ra E nằm giữa A và C.
Xét ΔABD và ΔAED, ta có:
AB = AE (theo cách vẽ)
∠(BAD) = ∠(EAD) (gt)
AD cạnh chung
Suy ra: ΔABD = ΔAED (c.g.c)
Suy ra: BD = DE (2 cạnh tương ứng)
và ∠(ABD) = ∠(AED) (2 góc tương ứng)
Mà: ∠(ABD) + ∠B1= 180o (2 góc kề bù)
∠(AED) + ∠E1= 180o (2 góc kề bù)
Suy ra: ∠B1= ∠E1
Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B
Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)
Suy ra: ∠E1> ∠C
Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Vậy BD < DC.

A B C E D 2 1 1 2 1 2
Lấy điểm E trên AC sao cho AE = AB.
Xét hai tam giác \(\Delta ABD\)và \(\Delta AED\),ta có :
AB = AE (gt)
\(\widehat{A_2}=\widehat{A_1}\)(vì AD là tia phân giác)
AD chung
Do đó : \(\Delta ABD=\Delta AED\left(c.g.c\right)\Rightarrow BD=DE\)
\(\widehat{B_1}=\widehat{E_1}\Leftrightarrow\widehat{B_2}=\widehat{E_2}\) (1)
Mặt khác,ta lại có : \(\widehat{B_2}>\widehat{C}\)(vì góc B2 là góc ngoài của tam giác ABC) (2)
Từ (1) và (2) suy ra : \(\widehat{E_2}>\widehat{C}\)
Khi đó trong \(\Delta CDE\)vì : \(\widehat{E_2}>\widehat{C}\Leftrightarrow CD>DE\Leftrightarrow CD>BD\)

a)
Vì tam giác ABC vuông tại A
=> AB<BC( Vì cạnh huyền lớn hơn cạnh góc vuông )
b) Kẻ DH⊥BCDH⊥BC
Xét ΔABD,ΔHBDΔABD,ΔHBD có :
⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩ˆBAD=ˆBHD(=90o)BD:chungˆABD=ˆHBD(BD là tia phân giác của góc B){BAD^=BHD^(=90o)BD:chungABD^=HBD^(AD là tia phân giác của góc B)
⇒ΔABD=ΔHBD(ch−gn)⇒ΔABD=ΔHBD(ch−gn)
⇒AD=DH⇒AD=DH (2 cạnh tương ứng) (1)
Xét ΔDHCΔDHC có :
ˆH=90o⇒DH<DCH^=90o⇒DH<DC ( cạnh góc vuông nhỏ hơn cạnh huyền) (2)
Từ (1) và (2) => DC>AD
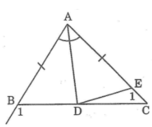
Lời giải:
Trên cạnh AC lấy điểm E sao cho AE = AB.
Ta có: AB < AC nên AE < AC
Suy ra E nằm giữa A và C.
Xét ΔABD và ΔAED, ta có:
AB = AE (theo cách vẽ)
∠(BAD) = ∠(EAD) (gt)
AD cạnh chung
Suy ra: ΔABD = ΔAED (c.g.c)
Suy ra: BD = DE (2 cạnh tương ứng)
và ∠(ABD) = ∠(AED) (2 góc tương ứng)
Mà: ∠(ABD) + ∠B1= 180o (2 góc kề bù)
∠(AED) + ∠E1= 180o (2 góc kề bù)
Suy ra: ∠B1= ∠E1
Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B
Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)
Suy ra: ∠E1> ∠C
Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Vậy BD < DC.
Trên cạnh AC lấy điểm E sao cho AE = AB
AB < AC nên AE < AC => E nằm giữa A và C
Xét ∆ABD và ∆AED:
AB = AE (theo cách vẽ)
\(\widehat{BAD}=\widehat{EAD}\left(gt\right)\)
AD cạnh chung
Do đó: ∆ABD = ∆AED (c.g.c)
=> BD = DE (2 cạnh tương ứng)
\(\Rightarrow\widehat{ABD}=\widehat{AED}\)(2 góc tương ứng)
\(\widehat{ABD}+\widehat{B_1}=180^0\)(2 góc kề bù)
\(\widehat{AED}+\widehat{E1}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{B_1}=\widehat{E_1}\)
Trong ∆ABC ta có\(\widehat{B_1}\)là góc ngoài tại đỉnh B.
\(\Rightarrow\widehat{B_1}>\widehat{C}\)(tính chất góc ngoài tam giác)
\(\Rightarrow\widehat{E_1}>\widehat{C}\)
Trong ∆DEC ta có:\(\widehat{E_1}>\widehat{C}\)
=>DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Suy ra: BD < DC