Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

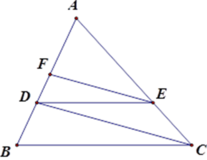
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C

Đáp án đúng là: A
Áp dụng định lí Thalès:
• Với DE // BC (E ∈ AC) ta có: \(\dfrac{{A{\rm{D}}}}{{AB}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{6}{{9}} = \dfrac{2}{3}\)
• Với EF // CD (F ∈ AB) ta có: \(\dfrac{{AF}}{{A{\rm{D}}}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{2}{3}\)
Suy ra: \({\rm{AF}} = \dfrac{2}{3}A{\rm{D}} = \dfrac{2}{3}.6 = 4(cm)\)
Vậy AF = 4 cm.

434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

ta có: DE// AC; D thuộc BC; E thuộc AB của tg ABC
=> AE/AB = CD/BC ( định lí Ta-lét) (*)
ta có: DF// AB ....
=> AF/AC = BD/BC ( định lí Ta-lét)
Từ (*) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{CD+BD}{BC}=\frac{BC}{BC}=1\)
hình tự vẽ
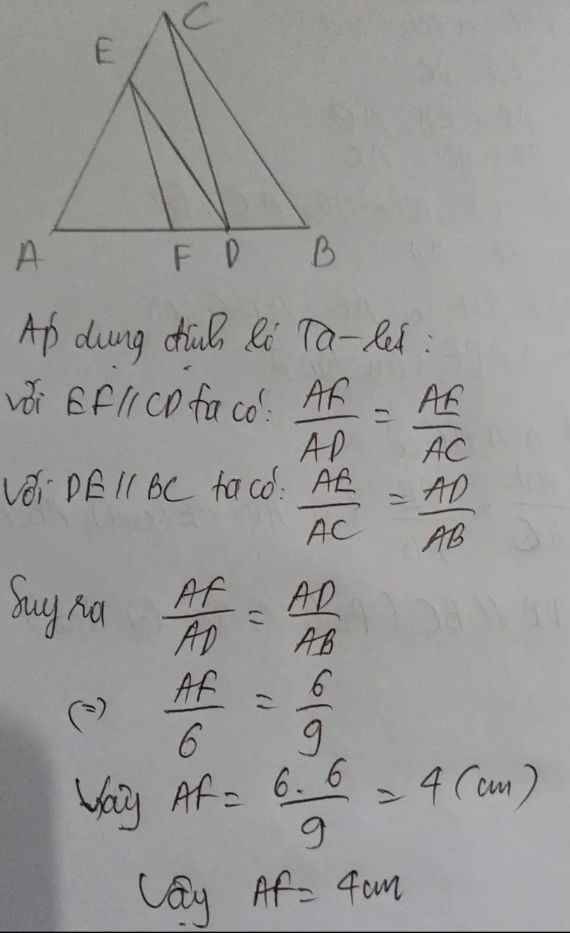
Áp dụng định lí Ta-lét:
+với EF//CD ta có \(\frac{AF}{AD}=\frac{AE}{AC}\)
+với DE//BC tác có \(\frac{AE}{AC}=\frac{AD}{AB}\)
suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\),
tức là \(\frac{AF}{6}\)\(=\frac{6}{9}\)
=> AF=\(\frac{6.6}{9}=4\left(cm\right)\)
CHÚC BẠN HỌC TỐT
Nguyễn Minh Hiếu ok
\n