Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét: Tam giác ABC có a2 + b2 = c2 nên vuông tại C.
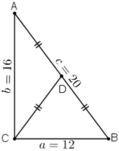
+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)
+ Chiều cao ha: ha = AC = b = 16.
+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.
+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.
Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.
+ Đường trung tuyến ma:
ma2 = (2.(b2 + c2) – a2) / 4 = 292 ⇒ ma = √292.

Áp dụng định lí Cosin, ta có B C 2 = A B 2 + A C 2 − 2 A B . A C . cos B A C ^
= 3 2 + 6 2 − 2.3.6. c o s 60 0 = 27 ⇔ B C 2 = 27 ⇔ B C 2 + A B 2 = A C 2 .
Suy ra tam giác ABC vuông tại B, do đó bán kính R = A C 2 = 3.
Chọn A.

Do tam giác ABC đều nên tâm đường tròn ngoại tiếp O trùng trọng tâm
Gọi AM là trung tuyến (kiêm đường cao), theo tính chất trọng tâm:
\(AM=\dfrac{3}{2}AO=\dfrac{3}{2}R=12\)
\(AM=\dfrac{AB\sqrt{3}}{2}\Rightarrow AB=8\sqrt{3}\)
\(S=\dfrac{1}{2}AM.AB=48\sqrt{3}\)
Tam giác ABC đều.
\(\Rightarrow AB=AC=BC\) (Tính chất tam giác đều).
Áp dụng định lý sin vào tam giác ABC đều, ta có:
\(\dfrac{a}{\sin A}=2R.\Rightarrow\dfrac{BC}{\sin60}=2.8.\Leftrightarrow BC=16.\dfrac{\sqrt{3}}{2}=8\sqrt{3}\) (đvđd).
\(\Rightarrow BC^2=192\) (đvđd).
Ta có: \(S=\dfrac{1}{2}ac.\sin B.\)
\(\Rightarrow S=\dfrac{1}{2}BC.AB.\sin60^o=\dfrac{1}{2}.BC^2.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4}.192=48\sqrt{3}\) (đvdt).