Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

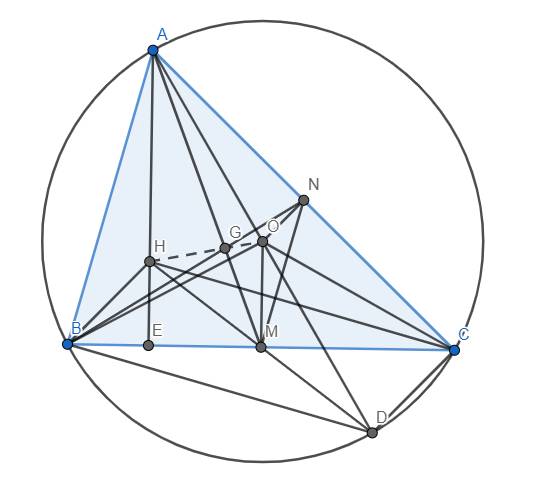
a) Ta chứng minh \(\Delta HAB~\Delta OMN\). Thật vậy, từ đề bài, dễ thấy H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác ABC. Vẽ đường tròn ngoại tiếp này. Dựng đường kính AD của (O). AH cắt BC tại E.
Ta thấy \(\widehat{ACD}=\widehat{AEB}\left(=90^o\right)\) và \(\widehat{ADC}=\widehat{ABE}\) (góc nội tiếp cùng chắn \(\stackrel\frown{AC}\)). \(\Rightarrow\Delta ACD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\widehat{BAH}=\widehat{CAO}\)
Mà \(\widehat{CAO}=\widehat{OCA}\), thêm vào đó tứ giác OMCN nội tiếp (vì \(\widehat{OMC}=\widehat{ONC}=90^o\)) nên \(\widehat{OMN}=\widehat{OCN}\). Do đó \(\widehat{HAB}=\widehat{OMN}\)
Hoàn toàn tương tự, ta suy ra \(\widehat{HBA}=\widehat{ONM}\). Từ đó suy ra \(\Delta HAB~\Delta OMN\left(g.g\right)\) (đpcm)
b) Ta thấy BH//CD\(\left(\perp AC\right)\) và CH//BD\(\left(\perp AB\right)\) nên tứ giác BDCH là hình bình hành. Mà M là trung điểm BC nên M cũng là trung điểm của DH. Lại có O là trung điểm của AD nên OM là đường trung bình của tam giác DHA \(\Rightarrow\left\{{}\begin{matrix}OM//AH\\OM=\dfrac{1}{2}AH\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{HAG}=\widehat{GMO}\\\dfrac{AH}{OM}=\dfrac{GA}{GM}\left(=2\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHG~\Delta MOG\left(c.g.c\right)\) (đpcm)
c) Từ \(\Delta AHG~\Delta MOG\Rightarrow\widehat{AGH}=\widehat{MGO}\)
Do A, G, M thẳng hàng nên \(\widehat{AGH}+\widehat{HGM}=180^o\)
Từ đó suy ra \(\widehat{HGM}+\widehat{MGO}=180^o\) \(\Rightarrow\) H, O, G thẳng hàng.

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

A B C D M N O I K P Q H S R L T E G
1) Do DN // AB nên ^DNC = ^BAC (Đồng vị). Mà ^BAC = ^DBC nên ^DNC = ^DBC => Tứ giác BNCD nội tiếp
Suy ra 5 điểm B,O,N,C,D cùng thuộc 1 đường tròn => ^BND = ^BOD = ^COD = ^CND
Ta có: DN // AB => ^BND = ^ABN. ^CND = ^NAB => ^NBA = ^NAB => \(\Delta\)ANB cân tại N (đpcm).
2) Ta có: ^DCM = ^DNB = ^DNC => \(\Delta\)DMC ~ \(\Delta\)DCN => DC2 = DM.DN. Dễ thấy: DC2 = DI.DA
Suy ra: DM.DN = DI.DA => Tứ giác AIMN nội tiếp => ^IMK = ^IAN = ^IBC => \(\Delta\)MIK ~ \(\Delta\)MKB (g.g)
=> KM2 = KI.KB. Ta lại có: ^KDI = ^IAB = ^KBD => \(\Delta\)IKD ~ \(\Delta\)DKB (g.g) => KD2 = KI.KB
Từ đó: KM2 = KD2 => KM = KD = DM/2. Do G là trung điểm KD nên \(\frac{GM}{GK}=3\) (1)
Gọi giao điểm của tia AD và tia ND là R. Theo hệ quả ĐL Thales: \(\frac{QB}{QM}=\frac{AB}{MR}\) (2)
Nếu ta gọi giao của PI với BC là V, theo phép vị tự thì I là trung điểm của PV. Từ đó suy ra: GM=GR
Mà GD = GK = GM/3 nên DK = MR/3. Lại áp dụng hệ quả ĐL Thales: \(\frac{IK}{IB}=\frac{DK}{AB}=\frac{MR}{3AB}\) (3)
Từ (1),(2),(3) suy ra: \(\frac{GM}{GK}.\frac{QB}{QM}.\frac{IK}{IB}=3.\frac{AB}{MR}.\frac{MR}{3AB}=1\). Theo đk đủ của ĐL Mélelaus thì 3 điểm Q,I,G tương ứng nằm trên các cạnh BM,BK,KM của \(\Delta\)BKM thẳng hàng (đpcm).
3) Gọi (HCS) cắt (O) tại điểm thứ hai là T. E là giao điểm của OD và BC.
Ta thấy: ^TBD = ^TCB = ^THS = ^THD (Góc tạo bởi tiếp tuyến và dây + Góc nội tiếp) => Tứ giác BHTD nội tiếp
Từ đó: 5 điểm B,H,E,T,D cùng thuộc 1 đường tròn => ^BTD = ^BED = 900
Mặt khác: ^DTE = 1800 - ^DBE = 1800 - ^BAC = ^BTC => ^DTE = ^BTC => ^BTD = ^CTE
Suy ra: ^CTE = 900 => T nằm trên đường tròn (CE) cố định. Mà T cũng thuộc (O) cố định.
Nên T là điểm cố định. Do đó: Dây CT của đường tròn (HCS) cố định
=> Tâm L của (HCS) luôn nằm trên đường trung trực của đoạn CT cố định (đpcm).

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC
đây nhé, cậu chịu khó tự vẽ hình vậy
câu a, ta có MN//AB(đường trung bình ) nên \(\widehat{MNC}=\widehat{BAC}\)
mà \(\hept{\begin{cases}\widehat{MNC}+\widehat{ONM}=90^o\\\widehat{BAC}+\widehat{ABH}=90^o\end{cases}}\) => \(\widehat{ABH}=\widehat{MNO}\)
b) kẻ \(BK⊥BC=B\) (K là giao của OC với BK)
ta có \(OM=\frac{1}{2}BK\Rightarrow O\) là trung điểm của KC=>ON //AK( đường tb)
mà ON//BH=>AK//BH và ta có BK//AH nên AKBH là hình bình hành => BK=AH => 2OM=AH
mà 2GM=AG =>\(\frac{GM}{OM}=\frac{AG}{AH}\) (1)
mặt khác ta có \(\widehat{HAM}=\widehat{OMG}\) (so le trong ) (2)
từ (1) và (2) =>tam giác AHG đồng dặng với tam giác MOG(ĐPCM)
c) dựa vào câu b nhé
dễ mà
a, ta có
tam giác ABH đồng dạng với tam giác MNO (g.g) (chứng minh = cách sd t/c cua 2 góc có cạnh t/ứ //)
=> AH/OM = AB /MN =2 => DPCM
b,Gọi giao điểm của HO và AM là G'
cần chứng minh G' trùng G
Ta c/m đc tam giác AG'H đồng dạng tg MG'O
=> AG' /MG' =AH/MO =2 => G' chia đoạn AM theo ti số 2:1 => G' là trọng tâm => G' trùng G
=> ĐPCM
vậy là 3 k nhé
*****