Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔHAC vuông tại H và ΔHDC vuông tại H có
CH chung
HA=HD
Do đó: ΔHAC=ΔHDC
Suy ra: CA=CD

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C

Ta có :O là trung điểm của BC(gt)
O là trung điểm của AK(OA=OK)
=>ABKC là hình bình hành(dhnb)
Mà góc BAC = 90 độ
=>ABKC là hình chữ nhật (dhnb)
=>AB=CK và góc ACK = 90 độ
Xét tam giác ABC và tam giác CKA có:
AB=CK(cmt)
góc BAC=góc KCA( cùng bằng 90 độ)
AC chung
Vậy tam giác ABC = tam giác CKA(c.g.c)
b)Xét tam giác AHB và tam giác CHA có
góc AHB = góc CHA (=90 độ)
góc BAH =góc ACH(cùng phụ với góc B)
Vậy tam giác AHB đồng dạng tam giác CHA(g.g)
=>\(\dfrac{AB}{AH}=\dfrac{AC}{CH}\)(1)
Ta có AH\(\perp\)CH
ED\(\perp\)CH
=>AH//DE
Xét tam giác ACH có
AH//DE
=>\(\dfrac{AE}{HD}=\dfrac{AC}{CH}\)
=>\(\dfrac{AE}{AH}=\dfrac{AC}{CH}\)(do AH=AD)(2)
Từ(1) và (2) => \(\dfrac{AB}{AH}=\dfrac{AE}{AH}\)
=>AB=AE(đpcm)

M A B C N H F D
a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD
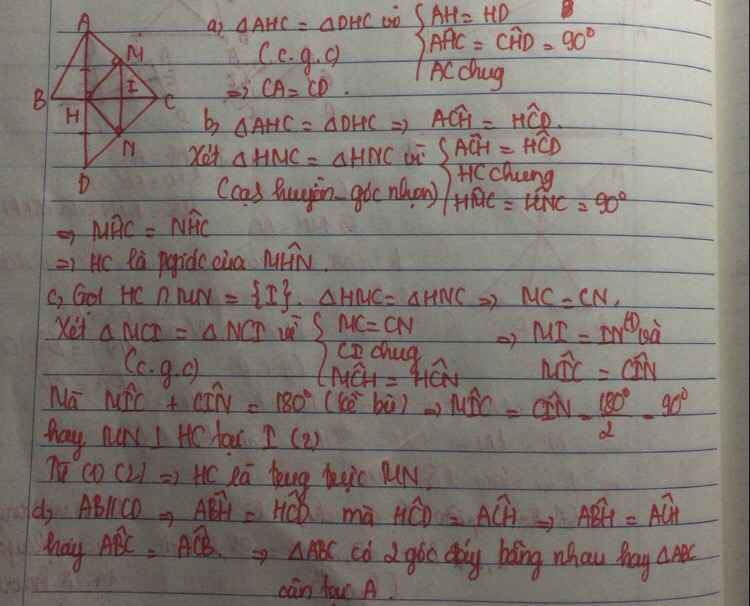
1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
giúp em khúc 2,3,4 với ạ; tất cả đều cùng 1 bài
1 thì em chưa học đến tam giác cân