Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
góc BAM chung
Do đó: ΔABM=ΔACN
2: XétΔBMC vuông tại M và ΔCNB vuông tại N có
BC chung
BM=CN
Do đó: ΔBMC=ΔCNB

`@` `\text {Ans}`
`\downarrow`
`1)`
Vì `\Delta ABC` cân tại A.
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABM` và `\Delta ACN`:
`\text {AB = AC}`
$\widehat {A} \text { chung}$
$\widehat {ANC} = \widehat {AMB} (=90^0)$
`=> \Delta ABM = \Delta ACN (ch-gn)`
`2)`
Xét `2 \Delta` vuông `BMC` và `CNB`:
$\widehat {B} = \widehat {C}$
`\text {BC chung}`
`=> \Delta BMC = \Delta CNB (ch-gn)`
`3)`
Vì `\Delta BMC = \Delta CNB (b)`
`-> \text {BN = CM (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AN + NB}\\\text{AC = AM + MC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BN = CM}\end{matrix}\right.\)
`-> \text {AM = AN}`
Xét `\Delta AMN`:
`\text {AM = AN}`
`-> \Delta AMN` cân tại A.
`4)`
Kẻ đường cao AI
Vì AI đi qua MN
`-> \text {AI} \bot \text {MN}`
Ta có: \(\left\{{}\begin{matrix}\text{AI }\bot\text{ MN}\\\text{AI }\bot\text{ BC}\end{matrix}\right.\)
`@` Theo tiên đề euclid
`-> \text {MN // BC}`
Hoặc bạn có thể giải cách này
Vì `\Delta AMN` cân tại A
\(\rightarrow\widehat{\text{AMN}}=\widehat{\text{ANM}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
Vì `\Delta ABC` cân tại A
\(\rightarrow\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`->` \(\widehat{\text{ABC}}=\widehat{\text{ANM}}\)
Mà `2` góc này ở vị trí sole trong
`-> \text {MN // BC (t/c 2 đt' //).}`
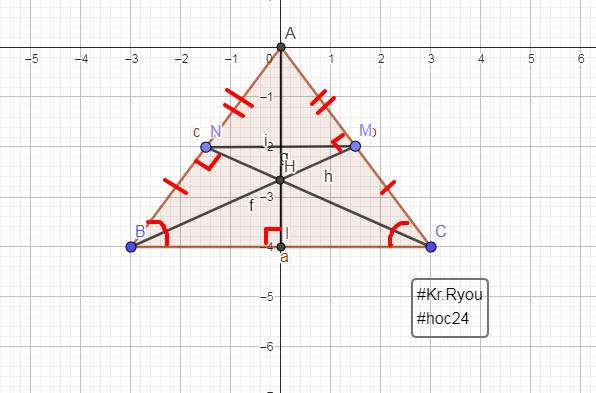
1: Xét ΔABM vuông tại M và ΔACN vuông tại N có
AB=AC
góc BAM chung
=>ΔABM=ΔACN
2: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
góc NBC=góc MCB
=>ΔNBC=ΔMCB
3: Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
4: AM/AC=AN/AB
=>MN//BC

\(a,ABM=MBC=\frac{ABC}{2}\)(BM là p/g t/g ABC)
\(ACN=NCB=\frac{ACB}{2}\)(CN là p/g t/g ABC)
mà ABC= ACB(t/g ABC cân A)
\(\rightarrow ABM=ACN\)
Xét t/g ABM và t/g ACN
Có ^BAC chung
AC= AB(t/g ABC cân A)
^ABM= ^ACN(cmt)
\(\rightarrow\)t/g ABM = t/g ACN(gcg)

a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...

1: Xét ΔABM và ΔACN có
\(\widehat{ABM}=\widehat{ACN}\)
AB=AC
góc A chung
Do đó: ΔABM=ΔACN
2: Xét ΔBMC và ΔCNB có
BM=CN
BC chung
MC=NB
Do đó: ΔBMC=ΔCNB