Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét 2 tam giác ABM=tam giác ACM(c.c.c)(tự cm)
nên góc AMB=góc AMC=180ddooj /2=90 độ
suy ra AM vuông góc vs BC

Trả lời:
P/s: Học kém Hình nên chỉ đucợ mỗi câu a
a, +Xét tam giác ABM và ACM có:
AB=AC(Giả thiết) --
AM là cạnh chung) I =>tam giác ABM=ACM (C-C-C)
~Học tốt!~

A B C E D I
Cm: Ta có : góc BAC + góc CAD = 1800 (kề bù)
=> góc CAD = 1800 - góc BAC = 1800 - 900 = 900 (1)
Và AD = AE (gt) (2)
Từ (1) và (2) suy ra t/giác AED là t/giác vuông cân tại A
b) Xét t/giác ABE và t/giác ACD
có AB = AC (gt)
góc BAC = góc CAD = 900(cmt)
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (hai cạnh tương ứng)
c) Gọi giao điểm của BE và DC là I
tự làm
d) tự làm

A B C E D M M
a) Vì AM là phân giác của góc BAC
nên góc BAM = CAM
Xét ΔBAM và ΔCAM có:
AB = AC ( giả thiết )
Góc BAM = CAM ( chứng minh trên )
AM cạnh chung.
=> Δ BAM = ΔCAM ( c.g.c )
=> BM = CM ( 2 cạnh tương ứng )
mà M nằm giữa B và C
Do đó M là trung điểm của BC → ĐPCM.
b) Ta có: AB + BE = AE
AC + CF = AF
mà AB = AC ( đề bài ); AE = AF (đề bài)
=> BE = CF.
Do ΔBAM = ΔCAM nên góc ABC = ACB ( 2 góc tương ứng )
Lại có: Góc ABC + CBE = 180 độ (kề bù)
Góc ACB + BCF = 180 độ (kề bù)
=> ABC + CBE = ACB + BCF
=> Góc CBE = BCF.
Xét ΔBCE và ΔCBF có:
BE = CF ( chứng minh trên)
Góc CBE = BCF ( chứng minh trên)
BC cạnh chung ( theo hình vẽ)
=> ΔBCE = ΔCBF ( c.g.c ) → ĐPCM.
c) Lại do ΔBCE = ΔCBF nên góc EBC = FCB ( 2 góc tương ứng ) hay góc EBM = FCM
Xét ΔMBE và ΔMCF có:
MB = MC ( chứng minh ở câu a )
Góc EBM = FCM ( chứng minh trên)
BE = FC ( chứng minh ở câu b)
=> ΔMBE = ΔMCF ( c.g.c )
=> ME = MF ( 2 cạnh tương ứng ) → ĐPCM.
d) Xét ΔEMN và ΔFMN có:
EM = FM ( chứng minh ở câu c )
EN = FN ( N là trung điểm EF )
MN chung.
=> ΔEMN = ΔFMN.
=> Góc ENM = FNM (2 góc tương ứng)
Suy ra MN là tia phân giác của góc ENF (1)
Có: góc BAM = CAM
Suy ra AM là tia phân giác của góc BAC (2)
Từ (1) và (2) suy ra A, M, N nằm trên cùng 1 đường thẳng.
Do đó A, M, N thẳng hàng → ĐPCM.
A B C M E F N
CM:a) Xét t/giác ABM và ACM
có: AB = AC (gt)
\(\widehat{BAM}=\widehat{CAM}\) (gt)
AM : chung
=> t/giác ABM = t/giác ACM (c.g.c)
=> BM = CM (2 cạnh t/ứng)
=> M là trung điểm của BC
b) Ta có: AE + AC = EC
AF + AB = FB
mà AE = AF (gt); AB = AC (gt)
=> EC = FB
Xét t/giác BCE và t/giác CBF
có: BC : chung
\(\widehat{BCE}=\widehat{FBC}\) (vì t/giác ABC cân)
EC = FB (cmt)
=> t/giác BCE = t/giác CBF (c.g.c)
c) Xét t/giác BEM và t/giác CFM
có: EB = FC (vì t/giác BCE = t/giác CBF)
\(\widehat{EBM}=\widehat{FCM}\) (vì t/giác BCE = t/giác CBF)
BM = CM (cm câu a)
=> t/giác BEM = t/giác CFM (c.g.c)
=> ME = MF (2 cạnh t/ứng)
d) Xét t/giác AEN và t/giác AFN
có: AE = AF (gt)
EN = FN (gt)
AN : chung
=> t/giác AEN = t/giác AFN (c.c.c)
=> \(\widehat{EAN}=\widehat{MAF}\) (2 góc t/ứng)
=> AN là tia p/giác của góc EAF => \(\widehat{EAN}=\widehat{MAF}=\frac{\widehat{EAF}}{2}\)
AM là tia p/giác của góc BAC => \(\widehat{BAM}=\widehat{CAM}=\frac{\widehat{BAC}}{2}\)
Mà \(\widehat{EAF}=\widehat{BAC}\) (đối đỉnh)
=> \(\widehat{EAN}=\widehat{NAF}=\widehat{BAM}=\widehat{MAC}\)
Ta có: \(\widehat{FAN}+\widehat{NAE}+\widehat{EAB}=180^0\)
hay \(\widehat{BAM}+\widehat{EAB}+\widehat{EAN}=180^0\)
=> A, M, N thẳng hàng
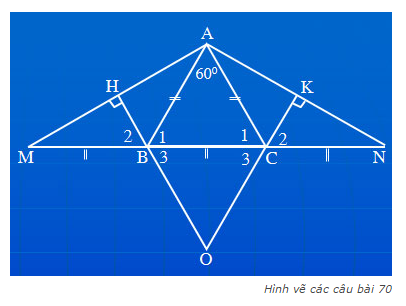
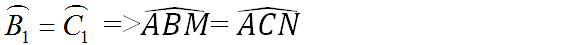
Sửa câu a thành CM: BM = CM
A B C D E M K
△ABC cân tại A ( BAC = 70o)
BAM = MAC = BAC/2
MD ⊥ AB (D AB) ;ME ⊥ AC (E
AB) ;ME ⊥ AC (E  AC)
AC)
ME = MK
KL
a, BM = CM
b, △DME cân
c, DE // BC
d, MDK = ?
Bài giải:
Vì △ABC cân tại A (gt) => AB = AC và ABC = ACB
Xét △BAM và △CAM
Có: AB = AC (cmt)
BAM = MAC (gt)
AM là cạnh chung
=> △BAM = △CAM (c.g.c)
=> BM = CM (2 cạnh tương ứng)
b, Xét △DBM vuông tại D và △ECM vuông tại E
Có: BM = MC (cmt)
DBM = ECM (cmt)
=> △DBM = △ECM (ch-gn)
=> DM = EM (2 cạnh tương ứng)
Xét △DME có: DM = EM (cmt) => △DME cân tại M
c, Vì △DBM = △ECM (cmt)
=> DB = EC (2 cạnh tương ứng))
Ta có: AD + DB = AB
AE + EC = AC
Mà AB = AC (cmt) ; DB = EC (cmt)
=> AD = AE
Xét △ADE có: AD = AE (cmt) => △ADE cân tại A => ADE = (180o - DAE) : 2 (1)
Vì △ABC cân tại A (gt) => ABC = (180o - BAC) : 2 (2)
Từ (1) và (2) => ADE = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> DE // BC (dhnb)
d, Ta có: ABC = (180o - BAC) : 2 (cmt)
=> ABC = (180o - 70o) : 2 = 110o : 2 = 55o
Mà ABC = ACB (cmt)
=> ACB = 55o
Xét △BMK và △CME
Có: BM = MC (cmt)
BMK = EMC (2 góc đối đỉnh)
MK = ME (gt)
=> △BMK = △CME (c.g.c)
=> MBK = MCE (2 góc tương ứng)
Mà MCE = 55o
=> MBK = 55o
Ta có: DBK = DBM + MBL = 55o + 55o = 110o
Lại có: DMB = EMC (△DBM = △ECM)
Mà EMC = BMK (2 góc đối đỉnh)
=> DMB = BMK
Ta có: MK = ME (gt)
Mà ME = DM (cmt)
=> DM = MK
Xét △BDM và △BKM
Có: BM là cạnh chung
DMB = BMK (cmt)
MD = MK (cmt)
=> △BDM = △BKM (c.g.c)
=> BD = BK (2 cạnh tương ứng)
=> △BDK cân tại B
=> BDK = (180o - KBD) : 2 = (180o - 110o) : 2 = 70o : 2 = 35o
Ta có: BDM + MDA = 180o (2 góc kề bù)
=> BDK + MDK + 90o = 180o
=> BDK + MDK = 90o
=> 35o + MDK = 90o
=> MDK = 55o
Cho tam giác ABC. Lấy D,E trên cạnh AB sao cho AD=DE=EB. vẽ DG và EF song song với BC (F và G thuộc AC)
a, chứng minh: AG=GF=FC
b, giả sử DG=3cm. Tính BC