Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

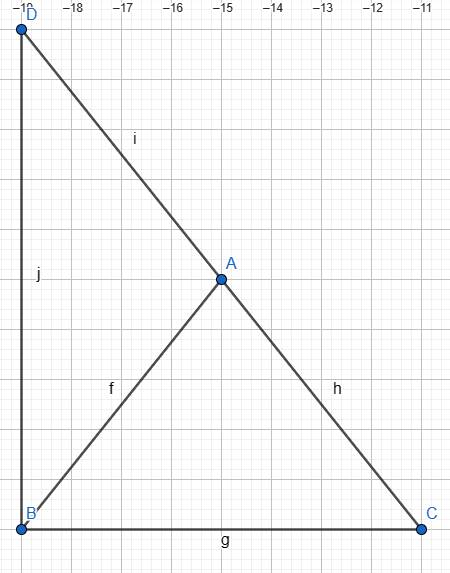
Sorri lỡ vẽ hình bự quá :D
\(\Delta ABC\) cân tại A => AB = AC (1)
D đối xứng với C qua A => A là trung điểm CD => AC = AD => AC=\(\dfrac{CD}{2}\)(2)
Từ (1) và (2) => \(AB=\dfrac{CD}{2}\)
Xét \(\Delta BCD\) có A là tđ CD => AB là trung tuyến
Mà \(AB=\dfrac{CD}{2}\) nên \(\Delta BCD\) vuông tại B
Độ dài cạnh CD: CD = 2.AB = 2.5 = 10 (cm)
Bây giờ áp dụng định lý Pytago để tính BD
Áp dụng đlý Pytago vào \(\Delta BCD\) vuông tại B ta có:
\(BC^2+BD^2=CD^2\\ =>6^2+BD^2=10^2\\ =>36+BD^2=100\\ =>BD^2=100-36=64\\ =>BD=\sqrt{64}=8\left(cm\right)\)
Diện tích \(\Delta BCD\): \(\dfrac{BD.BC}{2}=\dfrac{8.6}{2}=\dfrac{48}{2}=24\left(cm^2\right)\)
Vì đề k cho đơn vị nên mình để cm nha ![]()

a, Ta có: DE//BC \(\Rightarrow\widehat{DEB}+\widehat{EBF}=180\)
mà góc EBF =90 => góc DEB =90 (1)
Chứng minh tương tự với DF//AB
\(\Rightarrow\widehat{EDF}=90;\widehat{BFD}=90\) (2)
Từ (1) và (2) => tứ giác BEDF là hình chữ nhật
a) vì ED//BC và DF//AB
Mà \(\Delta ABC\)vuông tại B
Nên \(DE\perp AB\)và \(DF\perp BC\)
Xét tứ giác BEDF có:
\(\widehat{B}=\widehat{DEB}=\widehat{DFB}=90^0\)
Vậy tứ giác BEDF là hình chữ nhật

SABC = \(\frac{4\times6}{2}\) = 12 (cm2)
BH là đường cao của tam giác BAC cân tại B.
=> BH là đường trung tuyến của tam giác ABC.
=> H là trung điểm của AC.
=> AH = HC = AC/2 = 6/2 = 3 (cm)
Tam giác HBC vuông tại H có:
BC2 = HB2 + HC2 (định lý Pytago)
= 42 + 32
= 16 + 9
= 25
BC = \(\sqrt{25}\) = 5 (cm)
Tam giác HBC vuông tại H có HI là đường trung tuyến (I là trung điểm của BC)
=> HI = BC/2 = 5/2 = 2,5 (cm)
I là trung điểm của BC (gt)
I là trung điểm của HD (H đối xứng D qua I)
=> BHCD là hình bình hành.
mà BHC = 900
=> BHCD là hình chữ nhật.
=> BHCD là hình vuông
<=> BH = HC
<=> Tam giác BAC có đường trung tuyến BH bằng 1 nửa cạnh AC.
<=> Tam giác ABC vuông tại B.
mà tam giác BAC cân tại B.
=> Tam giác BAC vuông cân tại B.
Vậy BHCD là hình vuông khi tam giác BAC vuông cân tại B.

Bài 2:
Tam giác $ABC$ cân tại $A$ nên phân giác $AD$ đồng thời là đường cao
$\Rightarrow AD\perp DC$. Mà $\widehat{DAC}=\widehat{BAC}:2 =45^0$ nên $\triangle DAC$ vuông cân tại $D$
$\Rightarrow DA=DC(1)$
$D,E$ đối xứng với nhau qua $AC$ nên $AC$ là trung trực của $DE$
$\Rightarrow CD=CE; AD=AE(2)$
Từ $(1); (2)\Rightarrow AD=DC=CE=EA$
$\Rightarrow ADCE$ là hình thoi.
Mà $\widehat{ADC}=90^0$ nên $ADCE$ là hình vuông.

A B C D M K
a) Xét \(\Delta\)ABM và \(\Delta\)KCM có: MK = MA ; MB = MC ; ^AMB = ^KMC ( đối đỉnh )
=> \(\Delta\)ABM = \(\Delta\)KCM => AB = KC (1)
Vì \(\Delta\)ABC cân có AM là đường trung tuyến => AM là đường trung trực hay KM là đường trung trực => KB = KC(2)
\(\Delta\)ABC cân => AB = AC (3)
Từ (1) ; (2) (3) => AB = AC = KB = KC => ABKC là hình thoi
b) ABKC là hình thoi => KC //AB => CD //AB mà theo đề AD //BC
=> ABCD là hình bình hành
c) \(\Delta\)ABC cân có AN kaf đường trung tuyến => AM vuông góc BC mà AD // BC => AD vuông AM => ^DAK = ^DAM = 90 độ
Ta có: BM = 1/2 . BC = 6 : 2 = 3 cm AB = 5 cm
\(\Delta\)ABM vuông tại M . Theo định lí Pitago => AM = 4 cm
=> AK = 2AM = 2.4 = 8cm
AD = BC = 6cm ( ABCD là hình bình hành )
=> S ( DAK ) = AD.AK : 2 = 6.8 : 2 = 24 ( cm^2)
d) Để ABKC kaf hình vuông; mà ABKC là hình thoi nên ^BAC = 90 độ
=> tam giác ABC Có thêm điều kiện vuông tại A thì ABKC là hình vuông.

a: \(S_{ABC}=\dfrac{12\cdot10}{2}=60\left(cm^2\right)\)
b: Xét tứ giác AHBE có
M là trung điểm chung của AB và HE
góc AHB=90 độ
Do đó: AHBE là hình chữ nhật
c: Xét tứ giác ABFC có
H là trung điểm chung của AF và BC
AB=AC
Do đo: ABFC là hình thoi

a: Xét tứ giác ANBH có
M là trung điểm của AB
M là trung điểm của NH
Do đó: ANBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên ANBH là hình chữ nhật
cho em sửa đề lại là m và n lần lượt là trung điểm của cạnh AB và BC
dễ dàng chứng minh được BCD là tam giác vuông tại B
từ đó tính được BD
Có : SBCD = 1/2.BD.BC= 1/2.8.6 = 24
có : BA là đường trung tuyến của △BCD.
=> SABC = 1/2. SBCD =1/2. 24 = 12
Làm sao chứng minh B vuông vậy