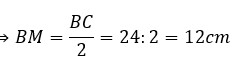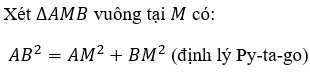Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lí Pytago:
`BC^2=AB^2+AC^2`
`<=>BC^2=3^2+4^2`
`<=>BC=5(cm)`
AM là đường trung tuyến của `\DeltaABC`
`=> AM = (BC)/2 = 5/2 (cm)`

Đây nè tự vẽ tự diễn nha
Vì AM VÀ BN LÀ 2 ĐG TRUNG TUYẾN
=> AN = 1/2 AC = 1/2 . 3 = 3/2
=> BM = 1/2 AB = 1/2 . 4 = 2
ĐẶT GN = X => GB = 2X ( TÍNH CHẤT TRỌNG TÂM)
GM = Y => GA = 2Y ( .....)
TAM GIÁC ANG VUÔNG TẠI N , THEO PYTAGO
GN^2 + GA^2 = AN^2
=> X^2 + (2Y)^2 = (3/2) ^2
=> X^2 + 4Y^2 = 9/4 (1)
tAM GIÁC GBM VUÔNG TẠI G THEO PY TA GO:
GM^2 + GB^2 = MB^2
=> Y^2+ ( 2X)^2 = 2^2
=> Y^2 + 4X^2 = 4
=> 4( Y^2 + 4X^2 ) = 4.4
=> 4Y^ 2 + 16X^2 = 16 (2)
lấY (2) - (1) TA CÓ 4Y^2 + 16 X^2 - X^2 - 4Y^2 = 16 -9/4
=> 15 X^2 = 55/4
=> X^2 = 11/12
TA CÓ X^2 + 4 Y^2 = 9/4 <=> 11/12 + 4 .Y^2 = 9/4 => 4Y^2 = 9/4 -11/2 =>4Y ^2 = 4/3 => Y^2 = 1/3
tAM GIÁC GAB VUÔNG TẠI g , THEO PY TA GO
(GA)^2 + (GB)^2 = AB^2
=> (2X)^2 + (2Y)^2 = AB^2
=>4X^2 + 4Y^2 = AB^2
=> 4( X^2 + Y^2 ) = AB^2
=> 4 ( 11/12 + 1 / 3) =AB^2
=> 4.5/4 = AB^2
=> AB^2 = 5
=> AB = CĂN 5

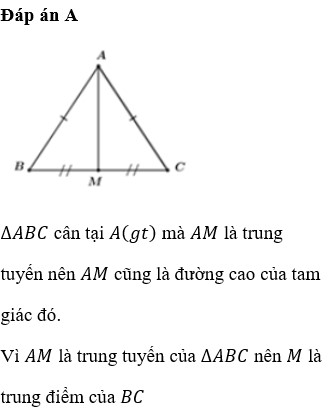
a, Xét tam giác ABC cân tại A có AM là trung tuyến
=> AM đồng thời là đường cao => AM vuông BC
b, Ta có BM = BC/2 = 3/2 cm
Theo định lí Pytago tam giác AMB vuông tại M
\(AM=\sqrt{AB^2-BM^2}=\dfrac{\sqrt{91}}{2}cm\)

a/
\(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5cm\) (Pitago)
b/
Ta có
\(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2,5cm\) (Trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
\(AG=\dfrac{2}{3}AM=\dfrac{2}{3}.\dfrac{5}{2}=\dfrac{5}{3}cm\) (trong tg 3 đường trung tuyến đồng quy tại 1 điểm và điểm đó cách đỉnh 1 khoảng bằng 2/3 độ dài đường trung tuyến mà trung tuyến đó đi qua)
c/
Xét tg ABN và tg CDN có
AN=CN (gt); BN=DN (gt)
\(\widehat{ANB}=\widehat{CND}\) (Góc đối đỉnh)
=> tg ABN=tg CDN (c.g.c)=> \(\widehat{BAN}=\widehat{DCN}=90^o\Rightarrow CD\perp AC\)

Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C