Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)ta có AB=AC
=)TAM giác ABC cân tại A
=)Góc B2=góc C1
Lại có B1+B2=180độ(kề bù)
C1+C2=180độ(kề bù)
mà B2=C1(cmt)
=)B1=C2
Xét tam giác ABM và tam giác ACN có
BM=CN(GT)
B1=C2(CMT)
AB=AC(GT)
=)TAM giác ABM = tam giác ACN (c-g-c)
=)AM=AN(2 cạnh tương ứng )
bạn tự viết kí hiệu nhá mik ko bít cách viết

A B C M N 1 2 2 1 E F 1 1 2 2 O
CM : a) Ta có: t/giác ABC cân tại A
=> góc B2 = góc C2
Mà góc B1 + góc B2 = 1800
góc C1 + góc C2 = 1800
=> góc B1 = góc C1
Xét t/giác AMB và t/giác ANC
có AB = AC (gt)
góc B1 = góc C1 (cmt)
MB = NC (gt)
=> t/giác AMB = t/giác ANC (c.g.c)
=> AM = AN (hai cạnh tương ứng)
=> t/giác AMN là t/giác cân tại A
b) Ta có: t/giác AMN cân tại A
=> góc M = góc N
Xét t/giác BME và t/giác CNF
có góc E1 = góc F1 = 900 (gt)
BM = CN (gt)
góc M = góc N (cmt)
=> t/giác BME = t/giác CNF (cạnh huyền - góc nhọn)
c,d) tự làm

a/
Ta có
\(\widehat{ABC}=\widehat{ACB}\) (2 góc ở đáy của tg cân ABC) (1)
\(\widehat{ABM}+\widehat{ABC}=\widehat{ACN}+\widehat{ACB}=180^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có
AB=AC (cạnh bên của tg cân ABC)
BM=CN (gt)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A
b/
Xét tg vuông BME và tg vuông CNF có
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\Rightarrow\widehat{AMN}=\widehat{ANM}\) (2 góc ở đáy của tg cân AMN)
BM=CN (gt)
\(\Rightarrow\Delta BME=\Delta CNF\) (Hai tg vuông có cạnh huyền và một góc nhọn tương ứng = nhau thì bằng nhau)
c/
Xét tg cân AMN có AM=AN (1)
\(\Delta BME=\Delta CNF\left(cmt\right)\Rightarrow ME=NF\) (2)
Từ (1) và (2) => AM-ME=AN-NF => AE=AF
Xét tg vuông AEO và tg vuông AFO có
AE=AF (cmt)
AO chung
\(\Rightarrow\Delta AEO=\Delta AFO\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau thì bằng nhau)
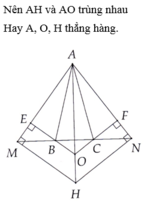
\(\Rightarrow\widehat{OAE}=\widehat{OAF}\) => AO là phân giác của \(\widehat{MAN}\)
d/
Ta có
\(\widehat{HMN}=\widehat{HMA}-\widehat{AMN}=90^o-\widehat{AMN}\)
\(\widehat{HNM}=\widehat{HNA}-\widehat{ANM}=90^o-\widehat{ANM}\)
Mà \(\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{HMN}=\widehat{HNM}\Rightarrow\Delta HMN\) cân tại H
Ta có
\(OE\perp AM;HM\perp AM\)=> OE//HM \(\Rightarrow\widehat{AOE}=\widehat{AHM}\) (góc đồng vị)
Chứng minh tương tự ta cũng có OF//HN \(\Rightarrow\widehat{AOF}=\widehat{AHN}\) (góc đồng vị)
Mà \(\Delta AEO=\Delta AFO\Rightarrow\widehat{AOE}=\widehat{AF}\)
\(\Rightarrow\widehat{AHM}=\widehat{AHN}\)=> HO là phân giác của \(\widehat{MHN}\)
Xét tg cân HMN có
HO là phân giác của \(\widehat{MHN}\)=> HO là đường trung trực của tg HMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(HO\perp MN\) tại trung điểm của MN
Xét tg cân AMN có
AO là đường phân giác của \(\widehat{MAN}\) (cmt) => AO là đường trung trực của tg AMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(AO\perp MN\) tại trung điểm của MN
=> AO trung HO (Từ 1 điểm trên đường thẳng chỉ duy nhất dựng được 1 đường thẳng vuông góc với đường thẳng đã cho)
=> A; O; H thẳng hàng

t lười vẽ hình lắm, vô cùng xin lỗi :(
a) Vì ∆ ABC cân tại A nên AH vừa là đường cao, vừa là trung tuyến => HB = HC = 12:2 = 6
Áp dụng định lí Py-ta-go cho ∆ AHB, ta được: AH2 + BH2 = AB2 => AB2 = 122 + 92 = 225 = 152 => AB = 15 = AC
=> PABC = AB + AC + BC = 15 + 15 + 18 = 48
b) Vì BM = CN (gt) ; HB = HC (cmt) => HB + BM = HC + CN => HM = HN => AH là trung tuyến của ∆ AMN (1)
Lại có: AH ┴ BC hay AH ┴ MN => AH là đường cao của ∆ AMN (2)
Từ (1) và (2) =>∆ AMN cân tại A
c) Xét ∆ BIM và ∆ CKN vuông tại I và K có:
MB = NC (gt) ; ^KNC = ^IMB (∆AMN cân tại A) => ∆ BIM = ∆ CKN ( ch - gn ) => MI = KN
Mà AM = AN (∆AMN cân tại A) => AI = AK => ∆ AIK cân tại A
=> ^AIK = ^AKI = ( 180o - ^MAN ) : 2 = ^AMN = ^ANM => IK // MN (đồng vị) hay IK // BC
d) Vì IK // MN => ^IKN = ^KCN (slt) ; ^KIB = ^IBM (slt)
Lại có: ^IBM = ^KCN ( vì ∆BIM=∆CKN ) => ^IKN = ^KIB hay ^OIK = ^OKI => ∆OKI cân tại O => OK = OI
Xét ∆ AIO và ∆ AKO có:
AI = AK ( ∆AIK cân tại A) ; OK = OI (cmt) ; AO (chung) => ∆ AIO = ∆ AKO ( c-c-c )
=> ^OAI = ^OAK (3)
Vì ∆AMN cân tại A => AH là phân giác của ∆AMN.=> ^HAM = ^HAN hay ^HAI = ^HAK (4)
Từ (3) và (4) => A, O, H thẳng hàng.
Ya, that's it!

B C A D E M N I H K
a) Ta thấy \(\widehat{ECN}=\widehat{ACB}\) (Hai góc đối đỉnh)
Tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\Rightarrow\widehat{ECN}=\widehat{DBM}\)
Xét tam giác vuông BDM và CEN có:
BD = CE
\(\widehat{ECN}=\widehat{DBM}\) (cmt)
\(\Rightarrow\Delta BDM=\Delta CEN\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow BM=CN\) (Hai cạnh tương ứng)
b) Do \(\Delta BDM=\Delta CEN\Rightarrow MD=NE\)
Ta thấy MD và NE cùng vuông góc BC nên MD // NE
Suy ra \(\widehat{DMI}=\widehat{ENI}\) (Hai góc so le trong)
Xét tam giác vuông MDI và NEI có:
MD = NE
\(\widehat{DMI}=\widehat{ENI}\)
\(\Rightarrow\Delta MDI=\Delta NEI\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow MI=NI\)
Xét tam giác KMN có KI là đường cao đồng thời trung tuyến nên KMN là tam giác cân tại K.
c) Ta có ngay \(\Delta ABK=\Delta ACK\left(c-g-c\right)\Rightarrow\widehat{ABK}=\widehat{ACK}\) (1) và BK = CK
Xét tam giác BMK và CNK có:
BM = CN (cma)
MK = NK (cmb)
BK = CK (cmt)
\(\Rightarrow\Delta BMK=\Delta CNK\left(c-g-c\right)\Rightarrow\widehat{MBK}=\widehat{NCK}\) (2)
Từ (1) và (2) suy ra \(\widehat{ACK}=\widehat{NCK}\)
Chúng lại là hai góc kề bù nên \(\widehat{ACK}=\widehat{NCK}=90^o\)
Vậy \(KC\perp AN\)